| :: La Storia: un mediatore culturale :: Origami
:: Moltiplicare divers(a)mente :: Etnomatematica
|
|
|

|
ETNOMATEMATICA
Nella
ricerca di materiale didattico che tenesse conto di
riferimenti culturali di diversi Paesi, mi sono imbattuta,
casualmente, nella lettura di alcuni articoli riguardanti l'etnomatematica.
Etnomatematica,
potrebbe far pensare a una matematica arretrata. Si è soliti
infatti, ritenere che la matematica abbia una sua
organizzazione razionale frutto di numerosi contributi ed
evolutasi nel tempo in modo lineare.
Il
termine Etnomatematica fu introdotto da un matematico
brasiliano, D'Ambrosio, nel 1985, facendo riferimento alla
" ..matematica praticata da popolazioni, gruppi
culturali ben identificabili, tribali, da gruppi di
lavoratori, classi professionali qualcosa che abbraccia tutti
i vari segmenti di una qualunque società, pertanto non potrà
essere visto come come qualcosa di unico né universale (1)
Questa
prima definizione può far cogliere la diversa prospettiva con
cui si osserva la disciplina ed è stata, per me, un'
autentica rivelazione. La sola lettura del libro
<Etnomatematica> di Marcia Ascher è sufficiente per
rimanere affascinati non solo dalla descrizione delle
<creazioni matematiche> di queste popolazioni, ma
soprattutto dalle implicazioni di carattere epistemologico,
storico e didattico di questi studi.
|
|

Ifa
divinazione M. W. McGinnis, 1996
|
UN
ESEMPIO: LE PRATICHE DIVINATORIE
Nel
libro della Ascher sono descritte alcune tradizioni in cui
importanti concetti matematici emergono dalle pratiche
quotidiane di popolazioni isolate geograficamente, ad esempio
nella creazione di calendari, nelle pratiche di
divinazione, nelle relazioni sociali o nelle decorazioni che
abbelliscono le soglie delle case.
Un
esempio è il conteggio mod 4 che regola le modalità
di divinazione praticata da una popolazione che vive nelle
Isole Caroline, un arcipelago del Pacifico settentrionale.
Lo
scopo di questa pratica è ottenere dalle divinità, tramite
la figura del divinatore, informazioni sulle vicende della
vita quotidiana, quali le questioni d'amore, di malattia, di
lavoro...
Lo
schema divinatorio è, in questo caso, abbastanza semplice:
uno spirito del destino è individuato da una coppia ordinata
di numeri (a,b) in cui a e b possono
assumere il valore di 1,2,3 o 4. Si possono così contare 16
spiriti diversi. Se si affiancano due coppie ordinate (a,b ) e
(a', b') si otterranno 256 accoppiamenti differenti, risultato
di 16 possibili spiriti del destino della prima coppia e 16
della seconda.
Ma
come sono determinati i numeri delle coppie? Con un meccanismo
casuale che richiede al cliente di scegliere in un mucchio
strisce di strisce realizzate con foglie di cocco, 4
strisce, a cui precedentemente sono stati fatti dei nodi a
caso.
Ogni
striscia viene messa fra le dita della mano e si inizia a
contare secondo l'aritmetica modulare, precisamente mod 4 (2)
Ad
esempio, se i nodi delle 4 strisce fossero, nell'ordine,
12, 7, 9, 15 si determinerebbe la combinazione (4, 3) (
5, 3) diversa dalla ( 5, 3) (4, 3)
Il
divinatore, figura onorata e ritenuta sacra, ha il compito di
interpretare le frasi determinate da questi accostamenti e
rispondere in questo modo alle domande dei richiedenti
La
divinazione Ifa, praticata dagli youruba della Nigeria, si
differenzia dalla precedente perché ogni risultato dà
origine ad un insieme di versi, a una frase e il cliente in
questo caso assume un ruolo attivo nella divinazione,
scegliendo quello che maggiormente ritiene adatto al suo
problema.
Anche
in questo caso, si utilizzano schemi numerici ottenuti
dalla manipolazione casuale di noci di palma o catene
divinatorie contenenti metà gusci di semi o di noccioli.
|


|
UN
ALTRO ESEMPIO: FIGURE SULLA SOGLIA
Queste
decorazioni prendono il nome di Kolam e sono realizzate
dalle donne del Tamil Nadu, nell'India meridionale. Le varie
forme possono riferirsi a occasioni speciali o semplicemente a
dare il benvenuto all'ospite. Sono eseguite da giovani donne
con farina di riso, che viene fatta scivolare, in modo
continuo, tra l'indice e il pollice con grande maestria,
seguendo schemi tramandati dalle madri, fino a poco tempo fa
soprattutto oralmente.
L'interesse
per questi disegni è rivolto al procedimento con cui si
costruiscono e alle modalità di memorizzazione.
L'osservazione
di una molteplicità di figure da parte di studiosi ha messo
in luce una grande varietà di tipi di kolam. In questi
insiemi di figure si possono però trovare alcune analogie che
riguardano l'impatto visivo ( presenza di simmetrie assiali e
rotazionali) e la procedura di esecuzione.
Per
disegnare un tipo di kolama come il pulli kolam si
inizia tracciando una una griglia di punti che ne
determina la configurazione. Nel primo caso (a) il kolam
si ottiene collegando i punti, nel secondo caso (b) tracciando
linee che girano attorno ad esse. Alcuni sono costituiti da
un'unica linea curva, altri da un numero limitato di curve
come queste


Nel
tentativo di capire come le donne tamil costruivano e
memorizzavano questi disegni, Gift Siromoney intorno al
1960 ha accostato l'informatica ai kolam, studiando i
linguaggi di immagini, linguaggi che generano immagini
attraverso algoritmi. Per analogia, basti pensare ai comandi
della <tartaruga> che lascia una traccia dopo aver
ricevuto i comandi relativi alla posizione e alla
direzione e iniziali, alla lunghezza del passo, all'ampiezza
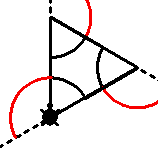
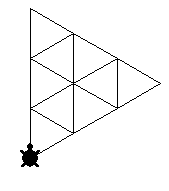
dell'angolo di rotazione. Ad esempio, se si vuole costruire un
triangolo equilatero occorre assegnare i comandi " AVANTI
100 DESTRA 120 e ripetere per 3 volte
E'
possibile memorizzare delle procedure che possono essere
richiamate per costruire forme modulari
Ma
la tartaruga disegna solo linee spezzate, chiuse o aperte,
pertanto gli studiosi, anche se in modo diverso, hanno dovuto
apportare delle modifiche per rappresentare figure curvilinee.
C'è chi ha smussato con tecniche particolari le figure
poligonali descritte dalla tartaruga e chi, come il gruppo di
lavoro di Siromoney ha apportato modifiche al linguaggio
cioè ai simboli e ai movimenti che assumono così il
seguente significato
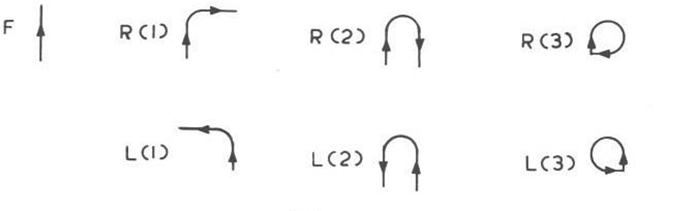 |
F:
muoviti avanti di una unità
R1
muoviti facendo mezzo giro a destra
R2
muoviti e fai una inversione completa a destra
R3
muoviti e facendo un cerchio completo a destra
L1,
L2 e L3: sono i corrispondenti movimenti di R1 R2 e R3 a
sinistra
|
I
kolam diventano una ricca fonte di figure che
potrebbero essere utilizzati come esempi di tipi di linguaggi
di immagini e servivano anche come stimolo per la creazione di
nuovi-
Le
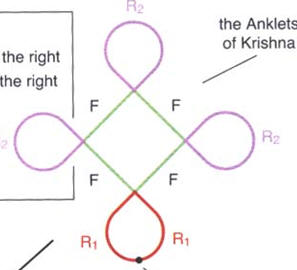
figure di seguito riportate, denominate cavigliere di Krishna,
sono curve chiuse che hanno caratteristiche comuni e sono
formate da copie di curve che si ripetono secondo un preciso
modello. Gli unici movimenti necessari sono : F, R1, R3.
| La stringa
iniziale è R1 F R3 F R3 F R3 F R1 |
|
|
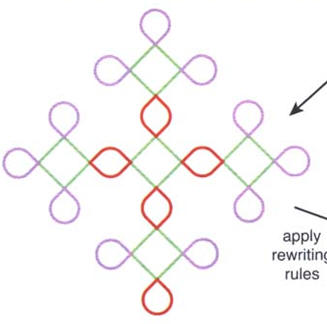
Il disegno successivo si
ottiene, a partire da quello iniziale, applicando questo
procedimento (3)
- a F si sostituisce
F (quindi F è una costante)
- a R1 si sostituisce la
stringa R1 F R3 F R1
- a R3 si sostituisce la
stringa R3 corrisponde
|
|
| |
|
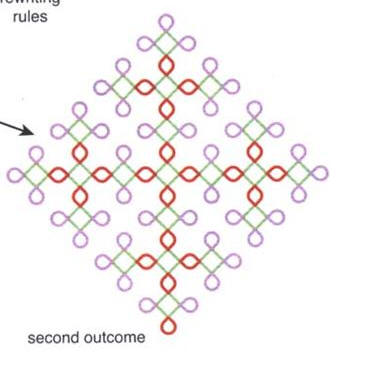
Si
può osservare che il tipo di crescita in questo insieme di
curve è esponenziale.
Il
numero dei fiori passa infatti da 1 a 4 a 16 a 64 ....
percorrendo così le potenze di 4
La
bellezza e la complessità di queste creazioni, continuano ad
appassionare matematici e informatici che si occupano di
linguaggi formali di immagini. Ma il libro della Ascher fa
scoprire anche una matematica che assume i contorni di un
modello di cooperazione, come nelle popolazioni basche, perchè
serve a garantire uguaglianza di condizioni individuali e di
ritmi di lavoro.
Conoscere
culture diverse, studiare i concetti matematici che le
attraversano, aiuta a " promuovere la comprensione del
fatto che i popoli di diverse tradizioni culturali
arricchiranno la stessa matematica portando in essa
prospettive differenti e modi diversi di percepire e
organizzare la visione del mondo"
|
| |
(1)
"Le matematiche degli altri" Radio3 Scienza.
Marco Motta ne parla con Franco Favilli, docente di
matematiche complementari all'università di Pisa.(11/09/2007)
(2)
Nell'insieme Z viene definita una relazione detta di "
congruenza modulo n" (con n ≥2) come a ≡ b (mod
n) se la differenza (a - b) è multiplo di n. Per esempio 13
≡ 1 (mod 4) .
Nel
caso si operasse in Z + , se a ≡ b (mod n) allora a e b,
divisi per n, danno lo stesso resto.
(3)
Si fa riferimento al Sistema-L introdotto e sviluppato dal
biologo olandese Aristid Lindenmayer che utilizzò questi
sistemi per descrivere ed analizzare l’accrescimento di
piante. Per approfondimenti. "Modelli
replicativi basati su sistemi di Lindenmayer e trasformazioni
di Möbius." Tesi di Sandra Pareschi
Università di Ferrara (2006-2007)
|
|
|