| :: La Storia: un mediatore culturale :: Origami
:: Moltiplicare divers(a)mente :: Etnomatematica
|
|
Origami I ragazzi cinesi sono
esperti e affascinano compagni e insegnanti con questi oggetti di
carta che nascono da un foglio e da ripetute e abili piegature. Come
non cogliere questa opportunità per arricchire l’esperienza
formativa di ciascuno, in particolare dei ragazzi che necessitano di
un supporto visuale per la comprensione di concetti geometrici!
Piegare la
carta, osservarne le tracce, motivare affermazioni, sono stati gli
obiettivi di questa attività. Per il docente è interessante scoprire
le leggi matematiche sottese agli origami, la loro supremazia nella
soluzione di problemi irrisolvibili con riga e compasso e
l'applicazione in diversi ambiti tecnologici, dai telescopi spaziali
agli airbag delle automobili (http://matematica.unibocconi.it/articoli/la-geometria-degli-origami)
Descrizione di alcune fasi dell' attività
|
1) Costruzioni
libere

|
I ragazzi in
questa fase sono impegnati a imparare per imitazione, acquisiscono dimestichezza con le diverse
fasi della piegatura e diventano consapevoli che
concentrazione e precisione sono indispensabili per ottenere
buoni risultati. |
| 2) Dal
rettangolo al quadrato

|
Basta una sola piega per ottenere un
quadrato partendo da un foglio rettangolare, ma ulteriori
pieghe lungo le diagonali e le linee mediane
possono essere utili per consolidare e visualizzare
proprietà di diversi <oggetti> geometrici quali : punto
medio, asse di un segmento, bisettrice di un angolo, asse di
simmetria.
Si scoprono inoltre le simmetrie del
quadrato, le isometrie che lo lasciano invariato e,
confrontando il quadrato con uno dei triangoli in cui è
diviso, si possono comporre simmetrie e rotazioni e
determinarne il loro prodotto
|
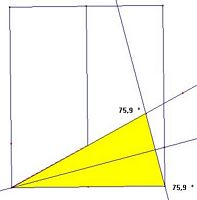
| 3) Dal
rettangolo al triangolo equilatero
 

 |
La costruzione è semplice e
sono gli errori commessi dai ragazzi che aiutano a
comprenderne la spiegazione. - Si
piega a metà il rettangolo in modo da far coincidere le due
parti e si tratteggia la piega ottenuta
- si fa scorrere un vertice (ad esempio
quello in basso a destra) lungo la linea tratteggiata fino a
che non si ottiene una piegatura che passa
contemporaneamente per la linea tratteggiata e per il
vertice in basso a sinistra.
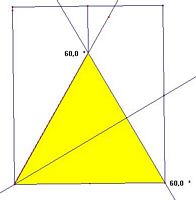
- abbiamo così evidenziati un lato,
l'altezza e la base ad essa relativa. Con altre due pieghe
si ottiene un triangolo equilatero. Ma è davvero equilatero?
Si può verificare in modo approssimativo,
manualmente, disponendo i triangoli affiancati. Si che vede
che 6 triangoli bastano per ricoprono lo spazio l'angolo
giro.
|
| 4) Da una figura è
possibile ottenere, sempre, un parallelogramma: come è possibile? Si prende un foglio
irregolare e con quattro piegature si costruisce un
quadrilatero convesso qualsiasi.
Si individuano, attraverso ulteriori
pieghe i punti medi di ciascun lato e si utilizza
un'applicazione il teorema di Talete
per ottenere
il parallelogramma. Basta infatti realizzare le pieghe che
congiungono i punti medi per ottenere il parallelogramma
desiderato
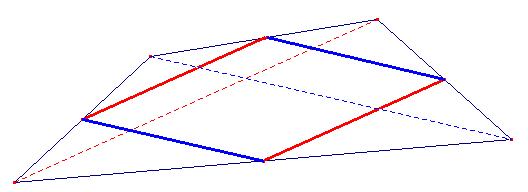
Dal Teorema di Talete discende infatti che
"in un
triangolo la retta condotta per il punto medio di un lato
parallelamente ad un secondo lato interseca il terzo lato
nel suo punto medio"
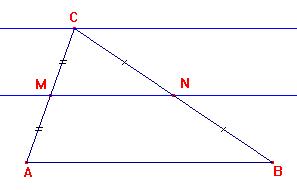
CM:MA=CN:NB
essendo CM=MA ne consegue che
anche CN=NB.
|
|
|