Costruzione di punti simmetrici rispetto ad una retta e individuazione di proprietà
Risorse, mezzi e strumenti
Foglio di carta bianca, Matita e matite colorate
Compasso, Righello, allegato 3_2c in
3_2 abcdefg Enclosures.pdf
Descrizione dell'attività
L’insegnante fa da guida agli alunni, sollecitando con domande, suggerendo come procedere nella manipolazione del materiale e come esporre con linguaggio appropriato le proprietà trovate.
L’insegnante spiega la consegna:dà istruzioni, mentre sollecita con domande gli alunni
disegna su un foglio bianco tre punti non allineati e denominali A, B, C
piega il foglio in modo che A, B, C stiano da una stessa parte della piegatura e indica con r la linea
con il foglio piegato lungo r, fai un foro con la punta del compasso in corrispondenza del punto A e chiama questo “foro” A’ ; fai la stessa operazione per i punti B e C.
unisci A con A’, B con B’ e C con C’.
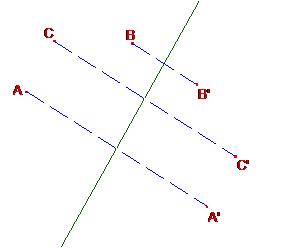
Guida gli alunni alla osservazione e alla individuazioni di proprietà
Che caratteristica hanno le rette contenenti i segmenti AA’ , BB’ e CC’?
Che caratteristica hanno tali rette rispetto alla retta r?
Misura la distanza da A ad r e da r ad A’; come sono fra loro queste distanze?
Misura la distanza da B ad r e da r a B’; come sono fra loro queste distanze?
Misura la distanza da C ad r e da r ad C’; come sono fra loro queste distanze?
Gli alunni con opportune domande vengono sollecitati alle seguenti osservazioni
Si guideranno gli alunni ad utilizzare un linguaggio più specifico:
il punto A simmetrico di A’ rispetto alla retta r
il punto B simmetrico di B’ rispetto alla retta r
il punto C simmetrico di C’ rispetto alla retta r
che equivalgono a:
i punti A e A’ sono simmetrici rispetto ad r
A’ è simmetrico di A rispetto ad r
A e A’ si corrispondono nella simmetria di asse r
A’ è il punto immagine di A nella simmetria di asse r.
Gli alunni saranno invitati a scrivere le 4 frasi equivalenti per i punti B e B’, C e C’.
Verranno sollecitati ad osservare relazioni di congruenza, parallelismo e perpendicolarità, per giungere alla descrizione delle proprietà
le rette contenenti i segmenti AA’ , BB’ e CC’ sono fra loro parallele
tali rette sono perpendicolari alla retta r
la distanza di A da r è uguale alla distanza di A’ da r
la distanza di B da r è uguale alla distanza di B’ da r
la distanza di C da r è uguale alla distanza di C’ da r
perciò la retta r è l’asse dei segmenti AA’, BB’, CC’.