La teoria dell’apprendimento che noi sposiamo è la teoria costruttivista. Anna Sfard ha mostrato come le teorie dell’apprendimento possano essere all’ingrosso separate lungo un crinale che da un lato vede quelle che si basano sulla metafora dell’«apprendimento come acquisizione» e dall’altro vede quelle che si basano invece sulla metafora dell’«apprendimento come acquisizione» (Sfard A.: 1991, On the dual nature of mathematical conceptions: reflections on processes and objects as different sides of the same coin, Educational Studies in Mathematics, 22, 1-36. Sfard A: 1999, Symbolizing mathematical reality into being: How mathematical discourse and mathematical objects create each other, in P. Cobb,K. E. Yackel, & K. McClain (Eds), Symbolizing and communicating: Perspectives on Mathematical Discourse, Tools, and Instructional Design (pp. 37-98). Mahwah, NJ: Erlbaum). Le teorie del primo versante si possono considerare come mentaliste nel loro orientamento, con un’enfasi sull’individuo che costruisce man mano le sue strutture cognitive in interazione con l’ambiente circostante. La teoria di J. Piaget ne è un esempio. Invece le teorie del secondo versante si basano sui contesti socio-culturali entro cui coloro che apprendono si trovano ad operare; si consideri la figura seguente:
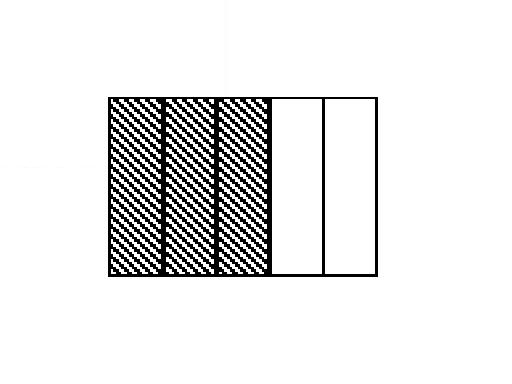
e si scriva la frazione che si pensa essa rappresenti. Molti scriveranno 3/5. Ma letta in modo diverso può rappresentare 1+2/3 (se si legge la parte scura come l’unità). Non c’è nulla inerente la figura che renda 3/5 la risposta “giusta”. Si scrive 3/5 perché quella è la frazione che tutti gli altri – insegnanti, autori di libri di testo, compagni di scuola – ci hanno insegnato a leggere; quindi quello è il modo socialmente accettato di interpretare la figura. Noi sposiamo la teoria costruttivista perché essa si situa esattamente sul crinale di separazione, avendo contemporaneamente aspetti mentalistici ed aspetti sociali.
La visione costruttivista dell’apprendimento sostiene da un lato che ogni individuo costruisce la sua propria raffigurazione della realtà a partire dalle sue proprie esperienze, dall’altro l’aspetto sociale del costruttivismo stesso enfatizza il ruolo della comunità costituita dalla classe (compagni più insegnante) nel fornire all’individuo quelle esperienze.
Per venire, come esempio, all’apprendimento della matematica, noi sosteniamo che coloro che apprendono non costruiscono una copia di una realtà matematica preesistente né che lavorano su «rappresentazioni interne» di una «rappresentazione fisica» di un concetto matematico. Le loro immagini mentali del concetto sono basate sulle esperienze fatte in classe ed in particolare sulle esperienze con le rappresentazioni utilizzate dall’insegnante. Comunque è necessario che l’insegnante sia conscio che non tutti gli allievi, a partire dalle stesse esperienze, formeranno immagini del concetto con la stessa velocità ed inoltre che alcuni possono non formare immagini mentali del tutto. E’ anche possibile che molti allievi non useranno la stessa immagine mentale dell’insegnante.
Per insegnare la matematica mentale ai ragazzi di scuola secondaria di primo grado, per esempio, occorre che essi siano in grado di formare immagini mentali adeguate. Per favorire la costruzione di tali immagini, che potranno poi essere utilizzate in future attività di pensiero, le attività in classe devono fornire le esperienze che possono più facilmente condurre alla formazione di quelle immagini ed incoraggiare la riflessione su di esse. La geometria fornisce esempi immediati di immagini visive mentali ed inoltre ci mostra come visualizzazioni fisiche particolari possano condurre a visualizzazioni mentali che restringono piuttosto che generare il corretto ambito del pensiero matematico del soggetto. Consideriamo ad esempio il seguente compito:

Immagina un triangolo ed una linea retta accanto al triangolo. Ora considera il simmetrico del triangolo immaginato rispetto alla retta immaginata.

Questo compito potrebbe rivelarsi come privo di senso per un soggetto che non abbia avuto le usuali esperienze scolastiche. Se un soggetto ha avuto una qualche esperienza nel disegnare figure piane simmetriche allora egli può essere in grado di formare una rappresentazione mentale del compito. Si può tuttavia riformulare il compito facendo riferimento alla riflessione in uno specchio o alla piegatura della carta. Comunque le “usuali esperienze scolastiche”, conducono spesso in errore, specialmente quando la simmetria è stata invariabilmente legata a rette di simmetria orizzontali o verticali. L’immagine mentale che si viene così a formare come risultato finale spesso conduce all’errore comune di immaginare il simmetrico come se la retta di simmetria fosse verticale o orizzontale (rispetto ad esempio alle righe di un foglio quadrettato) anche quando, invece, la retta forma un angolo con la verticale.
Per combattere questo errore occorre che l’attenzione di colui che apprende sia focalizzata sull’osservazione del processo di simmetrizzazione, occorre inoltre, ovviamente, che l’allievo lavori con diverse disposizioni di figure e rette di simmetria. Egli deve inoltre osservare con attenzione le caratteristiche delle relazioni tra le figure e le loro simmetriche. Potrà allora utilizzare queste diverse osservazioni per costruire l’oggetto matematico “simmetria” non come una semplice stereotipa visualizzazione, bensì come una comprensione delle sue caratteristiche. Il ruolo dell’insegnante è allora quello di sottoporre alla osservazione e allo studio degli alunni situazioni e costruzioni di simmetrie con figure diverse e con orientamenti diversi della retta di simmetria ed inoltre di educare alla osservazione delle caratteristiche delle relazioni fra figure e le loro simmetriche. Ciò può essere fatto attraverso la discussione, che avviene in piccoli gruppi di allievi e poi con tutta la classe, di esempi e controesempi incoraggiando i ragazzi a comunicare tra loro.