::
Introduzione
5_Equilibrium.pdf
::
Condizioni di equilibrio
:: Concetto di baricentro
::
Baricentro di figure regolari
:: Costruzione di oggetti in equilibrio
:: Proposta di verifica
|
|
Baricentro di figure regolari
| Finalità:
Concetto di baricentro – Baricentro di figure regolari e relazione con centro di simmetria – Base d’appoggio
Attività dell’insegnante: attraverso osservazioni guidate di oggetti presi dall’esperienza quotidiana l’insegnante farà di volta in volta individuare la posizione del rispettivo baricentro. Porterà poi i ragazzi a considerare figure geometriche regolari e ad individuare in questo caso la posizione del baricentro fino a giungere alla conclusione che essa coincide con il centro di simmetria.
Per quanto riguarda oggetti appoggiati definirà cosa si intende per base d’appoggio e attraverso osservazioni pratiche definirà la condizione di equilibrio di un corpo rigido appoggiato relativamente alla sua base d’appoggio.
Propone semplici costruzioni come attività operative per consolidare i concetti appresi.
Attività degli alunni: i ragazzi faranno osservazioni su oggetti di uso quotidiano; faranno costruzioni con riga e compasso; individueranno la posizione del baricentro nel caso di figure geometriche regolari.
Sperimenteranno l’equilibrio di corpi rigidi relativamente alla loro base d’appoggio (equilibrio del proprio corpo su un solo piede, pila di libri, ecc.).
Eseguiranno attività operative sotto la guida dell’insegnante
Risorse, strumenti: riga, squadra, compasso, lavagna.
|
|
Partiamo sempre dall’osservazione di oggetti presenti nell’esperienza quotidiana: il baricentro di una scala coincide con il suo punto medio, vicino al quale viene spontaneo mettere la spalla durante il trasporto; il baricentro di un coltello, invece, non sta nel punto medio, ma è spostato verso l’impugnatura, che il più delle volte pesa di più della lama.
E se un oggetto ha forma geometrica regolare?
Da quanto detto e sperimentato finora i ragazzi facilmente giungeranno alla conclusione che
in tutti i corpi aventi un centro di simmetria,
il baricentro coincide con il centro di simmetria |
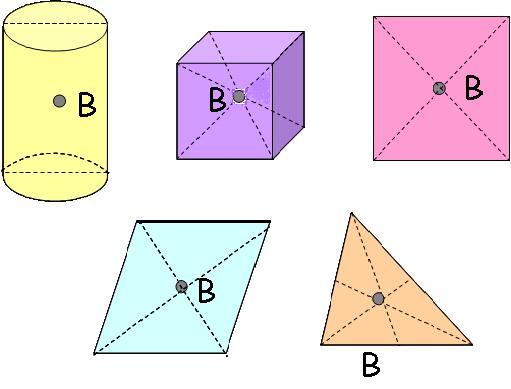
Così il baricentro di una sfera omogenea è il suo centro, quello di un cubo è l’intersezione delle diagonali. Analogamente il baricentro di un corpo laminare a forma di cerchio, o di rettangolo, o di rombo, oppure di triangolo equilatero è rispettivamente il centro del cerchio, l’intersezione delle diagonali e l’intersezione delle mediane.
Si potrà a questo collegare lo studio della geometria anche con l’ausilio del software didattico Cabrì per costruire figure geometriche regolari e individuarne il baricentro.
|
| Baricentro e base d’appoggio |
Anche noi cerchiamo di stare in equilibrio in modo da affaticare il meno possibile i nostri muscoli.
Ma perché è più facile stare in equilibrio con tutti e due i piedi ben appoggiati a terra?
Prova a stare su un piede solo: mettiti davanti ad uno specchio, cosa fai istintivamente?
Quando stiamo in piedi in posizione normale, i nostri piedi formano una base d’appoggio e il nostro baricentro si trova sopra a un punto che approssimativamente è in mezzo ai nostri piedi. Se alziamo il piede destro da terra , senza cambiare posizione, iniziamo a perdere l’equilibrio e ci rovesciamo. La spiegazione sta nel fatto che il nostro baricentro non è più sopra la base d’appoggio, che ora è il piede sinistro. Per riottenere l’equilibrio dobbiamo piegarci leggermente verso sinistra, in modo che la posizione del baricentro sia sopra il piede. Questo principio è valido per qualsiasi oggetto, da un acrobata, ad una roccia, alla pila di libri sulla scrivania ecc.
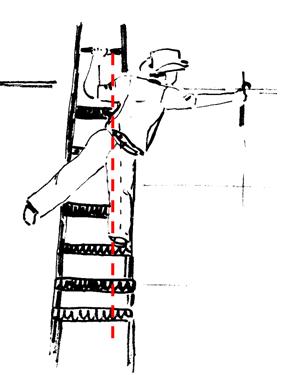
Anche se forse il suo comportamento è basato più sull’esperienza che sulla conoscenza fisica, l’uomo sulla scala sa cosa deve fare per evitare di cadere. Allungando la gamba all’indietro mentre si inclina in avanti, mantiene il baricentro posizionato sopra il piede che lo sostiene.
|
|
|
