Logo Simmetrie
nell'ambito di un progetto europeo
 
  Home Premessa Curriculum Approfondimenti Guida Piani di lezione Bibliografia    
    MAPPA  | SC. VITA | MATEMATICA  |  FISICA  |  CHIMICA  


  Equilibrio e simmetria  



 ::  Introduzione
5_Equilibrium.pdf

 ::  Condizioni di equilibrio

 :: Concetto di baricentro

 ::  Baricentro di figure regolari

 :: Costruzione di oggetti in equilibrio

 :: Proposta di verifica

 
Condizioni di equilibrio

Attività dell’insegnante

L’insegnante in questa fase guida i ragazzi alla definizione del concetto di equilibrio.
Più precisamente l’insegnante conduce gli alunni a definire le condizioni in cui si può affermare che un corpo (corpo rigido) è in equilibrio.

Attività degli alunni

Gli alunni, a partire dall’osservazione, esplicitano prima in un linguaggio comune e successivamente in un linguaggio più specifico le condizioni di equilibrio di un corpo.

Risorse, strumenti

Immagini proposte dall’insegnante, lavagna, asticella leggera, filo, cartoncini, forbici.

Esperienza 1: osserviamo le seguenti immagini (o disegni)
Si propongono immagini che mettono in evidenza la relazione fra simmetria ed equilibrio (tiro alla fune, bambino che sorregge alcuni libri, asta rigida, bilancia a bracci uguali, equilibrista,…).


Quando possiamo dire che siamo in una situazione di equilibrio?

Quando possiamo dire che un corpo è in equilibrio?


I ragazzi faranno le prime osservazioni:

“ Nel tiro alla fune se le squadre tirano con la stessa forza il punto centrale non si muove!”
“La bilancia è in equilibrio se mettiamo sui piatti masse uguali”
“Il bambino riesce a sorreggere la pila di libri fino a che ha la forza di reggerne il peso”







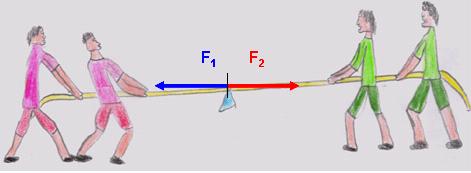
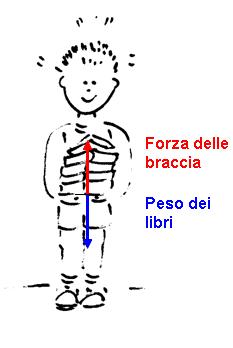
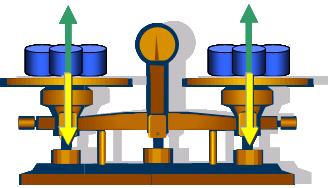
Sulle stesse immagini si rappresenteranno le forze come vettori, mettendo in evidenza che nella condizione di equilibrio la risultante delle forze è nulla: le forze “si equilibrano”.

Emerge la relazione con il concetto di simmetria

Osserviamo altre immagini: corpi che tendono a ruotare

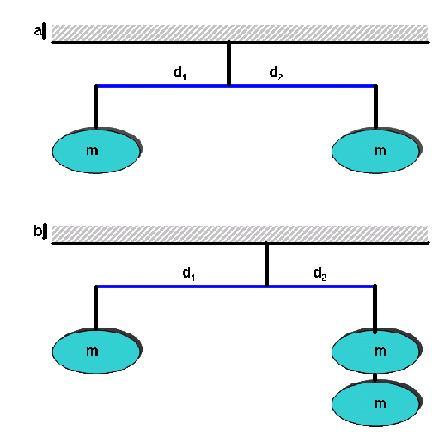
Si può costruire per esempio la composizione schematizzata nella figura seguente:

  1. Leghiamo un filo nel punto centrale di un’asticella leggera graduata
  2. All’estremo sinistro dell’asta leghiamo un oggetto di massa m, che può essere per esempio un cartoncino
  3. All’estremo opposto leghiamo un oggetto di uguale massa, m, per esempio un cartoncino uguale al primo
  4. Teniamo l’asta sospesa mediante il filo legato nel suo punto centrale: l’asta risulterà in equilibrio (vedi figura a)
  5. Ora ad uno degli estremi attacchiamo un secondo cartoncino, sempre uguale al primo (vedi figura b)
  6. Osserviamo che, per far in modo che l’asticella sia in equilibrio, dobbiamo spostare il punto di sospensione, cioè dobbiamo spostare la posizione del filo mediante il quale teniamo sospesa l’asticella

Dove sarà ora il punto di sospensione?

  1. Attacchiamo ora altri cartoncini , uguali tra loro, agli estremi dell’asticella. Ricerchiamo per ogni situazione la condizione di equilibrio spostando di volta in volta il punto di sospensione, e compiliamo la seguente tabella

Asticella in equilibrio


Numero cartoncini di massa m all’estremo sinistro
n1		 Distanza estremo sinistro dal punto di sospensione

d1		 Numero cartoncini di massa m all’estremo destro
n2		Distanza estremo destro dal punto di sospensione

d2
............
............
............
............

Attraverso l’osservazione dei risultati scopriremo che la condizione di equilibrio è esprimibile attraverso la relazione

n1 d1 = n2 d2

Anche in questo caso faremo notare la simmetria, che non si manifesta tanto attraverso l’osservazione visiva del sistema in equilibrio, quanto piuttosto dall’esplicitare le condizioni di equilibrio attraverso una relazione matematica.

Nota per l’insegnante:
Vanno sottolineate a questo punto l’importanza e l’efficacia del linguaggio matematico per esprimere i processi di astrazione richiesti dalla fisica. Lo sviluppo di capacità di formalizzazione e astrazione rappresenta del resto uno degli obiettivi principali dell’insegnamento scientifico.
In generale, le leggi della fisica si riferiscono a sistemi ‘ideali’ o comunque ‘schematizzati’. In questo senso, come già discusso, il fenomeno o l’oggetto ‘concreti’ sono trattati fisicamente attraverso ‘modelli’. Il passaggio ad una formalizzazione matematica del concetto fisico ha portato spesso alla comprensione più profonda del fenomeno stesso. Talvolta i modelli di diversi sistemi fisici possono presentare profonde analogie ‘formali’, in quanto si basano sulle stesse strutture matematiche. Una stretta connessione tra la matematica e la fisica può permettere di individuare e sfruttare queste analogie.




Nota: non si ritiene opportuno a questo livello specificare la definizione di momento torcente (o momento di una forza) a livello di linguaggio. Ci si può limitare all’osservazione di ciò che accade in situazioni facilmente riproducibili nell’esperienza quotidiana.

Attraverso le osservazioni precedenti si porteranno i ragazzi alla seguente definizione di condizione di equilibrio:

diremo che un corpo rigido inizialmente fermo è in equilibrio se
non tende a spostarsi e non tende a ruotare