::
Introduzione
5_Equilibrium.pdf
::
Condizioni di equilibrio
:: Concetto di baricentro
::
Baricentro di figure regolari
:: Costruzione di oggetti in equilibrio
:: Proposta di verifica
|
|
Concetto di baricentro
Finalità Introduzione al concetto di baricentro e definizione di equilibrio stabile,
instabile e indifferente
Attività operativa : Costruzione di oggetti che stanno in equilibrio
Risorse, strumenti: cartoncino, forbici, spago, un piccolo peso, matita e righello
Attività dell’insegnante: attraverso l’attività di costruzione di oggetti
che stanno in equilibrio in determinate condizioni, guida gli alunni alla comprensione dei concetti di baricentro,
equilibrio stabile, instabile e indifferente.
Attività degli alunni: gli alunni eseguono
le attività operative sotto la guida dell’insegnante. Esplicitano poi verbalmente,
in un linguaggio comune e successivamente più specifico i concetti relativi all’equilibrio.
Abbiamo visto che conoscere solamente il valore del peso (della forza-peso) non è sufficiente per stabilire se
un oggetto (appoggiato o sospeso) si trova in equilibrio o meno. Due corpi rigidi con lo stesso peso, ma con
forme diverse, in generale non sono sottoposti alle stesse condizioni di equilibrio.
In linea di principio, per sapere come mantenere in equilibrio un corpo rigido è necessario conoscere la sua
forma che, però, spesso è molto complicata.
In realtà si scopre che per ogni corpo rigido si può definire un punto, detto centro di gravità o baricentro,
in cui, per quanto riguarda la determinazione delle condizioni di equilibrio, è possibile considerare
concentrato tutto il peso dell’oggetto.
Si può affrontare questo nuovo concetto con una facile attività operativa.
|
| Esperienza 1: come trovare il baricentro |
SE SI TRATTA DI UNA FIGURA IRREGOLARE,
COME SI TROVA IL BARICENTRO?
Materiali occorrenti: cartoncino, forbici, spago, un piccolo peso, matita e righello.
Costruiamo con il cartoncino una figura irregolare e proviamo a mantenerla in equilibrio su di un dito,
come nel disegno seguente:

Come facciamo ad individuare il punto esatto del cartoncino in cui dobbiamo puntare
il dito affinché il cartoncino stesso rimanga in equilibrio?
Definiremo allora questo punto, detto centro di gravità o baricentro, in cui, per quanto riguarda
la determinazione delle condizioni di equilibrio, è possibile considerare concentrato tutto il peso dell’oggetto
Proviamo ora a trovare questo punto sul nostro cartoncino di forma geometrica irregolare:
Procedimento
- Appendiamo al muro con un chiodo il cartoncino di forma geometrica irregolare
- Leghiamo uno spago al chiodo; all’estremità opposta leghiamo il peso ottenendo un filo a piombo
- Lasciamo oscillare il cartoncino sospeso al chiodo finché non si ferma
- Il filo a piombo segna la linea verticale dal punto di sospensione: tracciamolo con la matita sul cartoncino
- Facciamo un foro in un altro punto del cartoncino e ripetiamo i punti 4 e 5.
Le due linee disegnate si incontrano in un punto: il baricentro
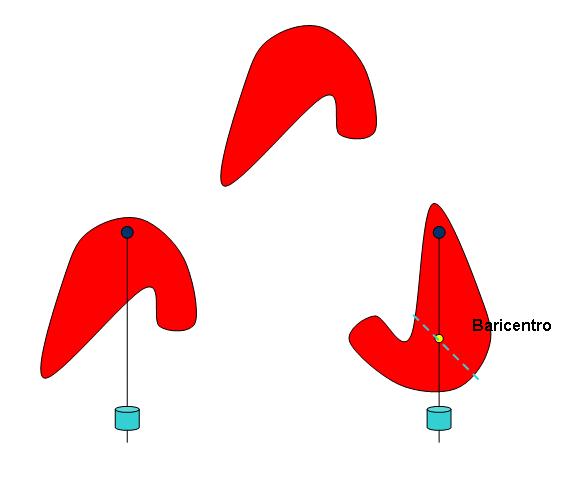
Come prova, foriamo il cartoncino in quel punto e appendiamolo al chiodo:
il cartoncino rimarrà in equilibrio in qualsiasi posizione lo giriamo
Osservazione. Non è detto che il baricentro di un corpo rigido sia un punto del corpo stesso.
Per esempio, se consideriamo una ciambella il suo baricentro è nel suo centro, dove non c’è materia.
|
| Esperienza 2: diversi tipi di equilibrio |
Ora che abbiamo introdotto il concetto di baricentro individuiamo
i diversi tipi di equilibrio.
In effetti l’equilibrio di un corpo può essere di tre tipi: stabile, instabile e indifferente.
Vediamo di cosa si tratta. Consideriamo un quadro appeso alla parete: esso è in equilibrio
(non può cadere perché il chiodo glielo impedisce, in quanto vincolo del quadro) e non ruota,
anche se la parete è molto liscia e quindi priva di attrito. Se spostiamo leggermente il
quadro da questa posizione, esso tende a ritornarvi (ovvero, spostato il corpo dalla posizione
di equilibrio in un’altra posizione vicina, il momento risultante delle forze esterne tende a riportarlo
nella stessa posizione di equilibrio). Allora quando un sistema in equilibrio si comporta in questo modo
diciamo che tale equilibrio è stabile.
Potremmo anche ruotare il quadro verso l’alto, mettendolo a testa in giù sopra il chiodo, e con un po’ di
fatica riusciremmo a trovare una posizione di equilibrio. Ma appena esso si sposta anche di pochissimo da
quella posizione comincia a ruotare attorno al chiodo fino a riportarsi nella posizione di equilibrio di prima.
Allora quando accade una situazione di questo tipo si dice che l’equilibrio è instabile.
Infine potremmo appendere il quadro proprio nel suo baricentro: in questo caso esso manterrebbe qualunque
inclinazione data. Se, partendo dall’equilibrio, lo spostassimo leggermente, esso non tenderebbe né a ritornare
sulla posizione di partenza, né a ruotare verso un’altra situazione di equilibrio, ma manterrebbe semplicemente
la nuova posizione. Allora quando ciò accade si dice che l’equilibrio è indifferente.
Come regola generale allora possiamo affermare che
per un corpo pesante, l’equilibrio è stabile, instabile e indifferente se un piccolo spostamento dalla posizione
di equilibrio tende rispettivamente ad innalzare o abbassare o lasciare il baricentro alla stessa altezza |

In applicazione di quanto appreso sopra, si può assegnare ai ragazzi la seguente ricerca per casa:
portare a scuola il bicchiere più stabile e quello meno stabile che essi possono individuare nelle loro cucine.
|
|
|
