| :: Premessa
:: Le parole a volte ingannano
:: I quadrati e le isometrie
:: Criteri meno austeri
:: Matematica con poche parole |
|
Matematica con poche parole Se non si conoscono le parole,
il materiale più o meno strutturato viene in aiuto per favorire
l'acquisizione di concetti. Ho prestato attenzione che i sussidi
fossero semplici, e privi di quegli "elementi di disturbo"
che spesso sono responsabili della formazione di misconcetti. La scelta e la manipolazione del
materiale hanno avuto principalmente lo scopo di attivare e
stimolare la concettualizzazione e solo raramente è stato impiegato
per concretizzare un concetto astratto.
|
 |
Spago, elastici
e strisce per costruire poligoni articolabili con cui vedere
come cambia il perimetro e l'area, stuzzicadenti per
visualizzare il rapporto fra segmenti: sono i materiali
<stra-economici> attraverso i quali Emma Castelnuovo ha
fatto scoprire a studenti e docenti una matematica più viva.
|
 |
Tanti cubi, alcuni singoli,
altri incollati in modo da formare cubi e parallelepipedi
diversi a base quadrata; si usano
per visualizzare e confrontare il volume, valutare la variazione della superficie
di parallelepipedi, a parità di
volume.
La scuola dispone inoltre di materiale che
risale a diversi anni fa, una sorta di precursore del Polydron.
Archi e aste flessibili, viti, giunture si sono rivelate
molto utili per costruire e osservare lo <scheletro> di solidi di
diversa forma,memorizzare termini, individuare relazioni fra
spigoli, vertici, facce, determinare sezioni di poliedri e
di solidi di rotazione.
|
 |
Ogni alunno
costruisce il proprio dispositivo e viene lasciato
libero di manipolarlo. Confrontandolo con quello dei compagni
si accorge facilmente che due semirette con l'origine in comune individuano due
angoli e che l'ampiezza di un angolo non dipende dalla
lunghezza dei lati. Si confrontano le ampiezze, si
stimano le misure e si interviene solo per evitare che
l'alunno diventi dipendente dal materiale; basta metterlo
nelle condizioni di coglierne la limitatezza, ad esempio
indicando un punto esterno allo strumento e chiedergli se
appartiene o meno ad uno degli angoli rappresentati. |
|
 |
La proprietà invariantiva
della sottrazione Aggiungendo o
togliendo...
|
|
 |
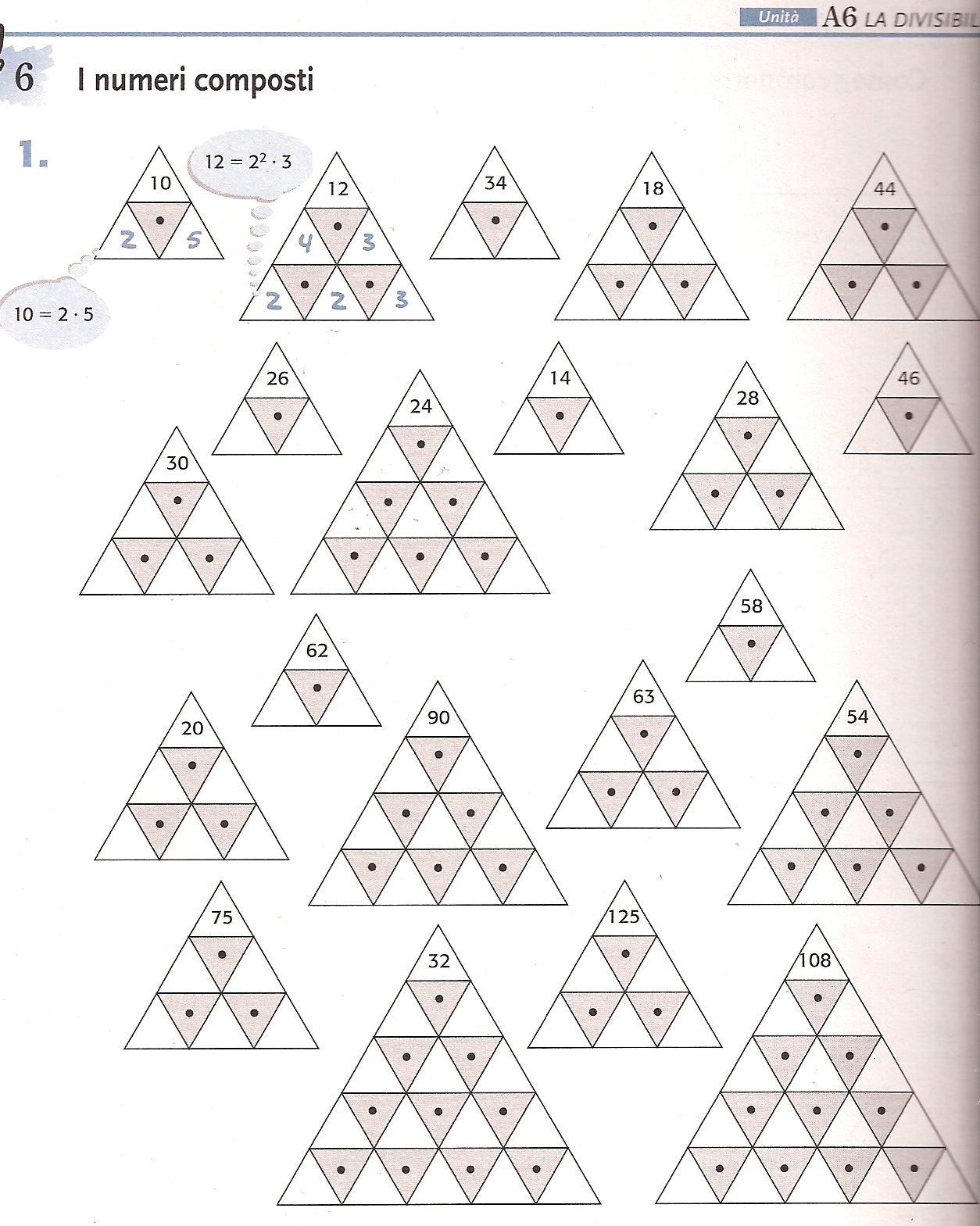Sono della
stessa autrice del testo di matematica in adozione questi
fascic oli
che contengono numerosi esercizi e
attività, spiegati con un linguaggio essenziale e
spesso <senza parole> come indicato nel titolo. |
|
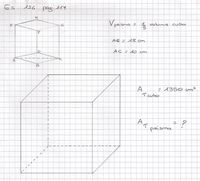
(dal sito
http://www3.ti.ch/) (dal testo
in adozione) |
Problemi senza parole:
facciamo tradurre il testo ai compagni così tutto si
semplifica, a parte la ricerca della soluzione! |
|
|
