La Torre di Hanoi

L'attività si è svolta con queste modalità

1)Comprensione delle regole: ho messo a disposizione 3 pioli e un certo numero di anelli (inizialmente 4) concentrici che devono essere infilati in ordine decrescente in uno dei pioli. Vince chi per primo riesce a spostare gli anelli in un altro piolo, con il vincolo di spostarne uno alla volta e disporlo al di sopra di un anello che deve essere più grande. Si gioca a coppie. 

2)Raccolta dati: Si invitano i ragazzi a disputare 3 gare in un tempo prestabilito. Si chiede ai ragazzi di scrivere a fianco del vincitore quante mosse ha utilizzato

3)Osservazione dei risultati: nella lettura dei risultati compare che ci sono vincitori più bravi di altri: quelli che hanno vinto con sole 15 mosse. Ho chiesto se qualcuno è in grado di vincere con un numero di mosse inferiore. Ma nessuno è parso interessato a seguirmi, convinti che le tante prove sperimentali abbiano un valore di certezza.

4)Variazione di un elemento del gioco: Ho chiesto allora di usare 3 anelli e di provare a vedere se c'era un vincitore fra i vincitori, quello che cioè che avrebbe vinto con il minor numero di mosse. Tutti comprendono e convengono che il numero minimo di mosse per vincere con 3 anelli sia 7. E si accorgono che esiste un numero minimo di mosse anche per i 4 anelli. Quello che sembrava poco interessante prima, in un momento successivo cattura  l'attenzione di molti.

5)Per sollecitarli a trovare il numero minimo di mosse con 5 anelli sono costretta a posticipare una verifica scritta. Si dividono in gruppi di 4: due giocano e gli altri due contano le mosse.

6)Si raccolgono i risultati e si dispongono in una tabella e molti riconoscono la regolarità della successione: 1,3,7,15,31

Ecco cosa scrivono i ragazzi:

Anche in questo caso la supremazia dei simboli, rispetto al linguaggio naturale è evidente

 m (con n anelli) = 2* m (con n-1 anelli) +1

provo a sintetizzare con

m _a= 2 * m _(a-1) + 1 ma senza molto successo

L'individuazione di regolarità si  può ampliare anche con questo problema: 

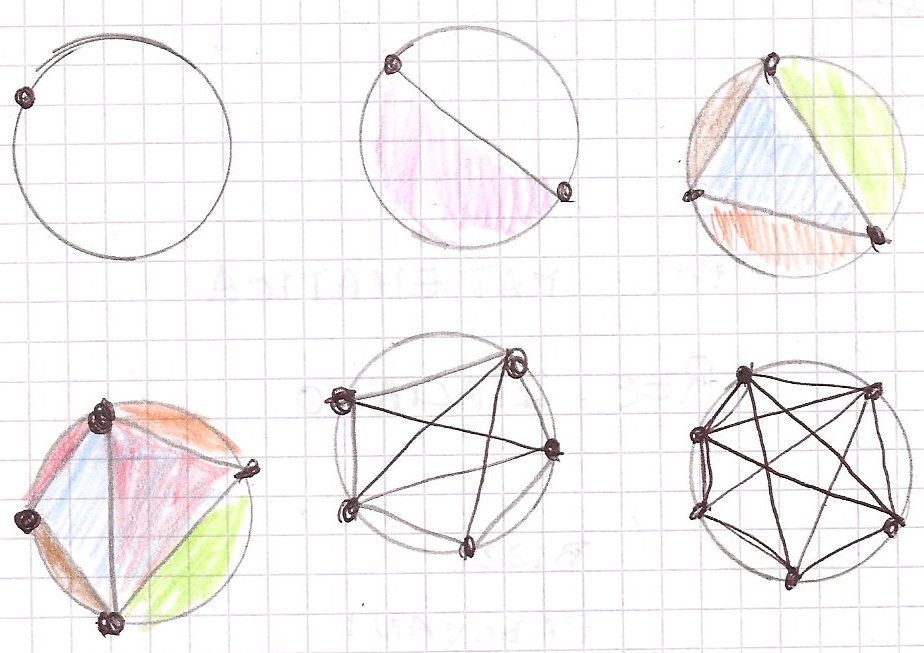
Disegna una circonferenza e segna due punti. Se collego questi punti il cerchio viene suddiviso in 2 parti (regioni). E se ne disegno 3 di punti, quante regioni ottengo? e 4?  Raccogli i risultati in una tabella e scrivi le tue osservazioni. Sai prevedere quante regioni si ottengono con 5 punti? e 6 punti? Verifica il risultato contandole.   

n° punti (2) n° regioni (2)

n° punti (3) n° regioni (4)

n° punti (4) n° regioni (8)

n° punti (5) n° regioni (?)

n° punti (6) n° regioni ( ?)