:: Introduzione
:: Perché le bolle
sono sferiche
:: Il commesso
viaggiatore
:: Lamine di sapone
e schiume
:: Collegamenti e
approfondimenti
|
|
Perché le bolle hanno forma sferica?
| La forma delle bolle non dipende dal telaio |
 Si potrebbe pensare che la forma sferica delle bolle di sapone dipenda dalla forma del telaio che viene usato per crearle.
Proviamo a fare telai di forma diverse e vediamo come vengono le bolle!!!
Questo semplice controesempio mostra che la forma sferica della bolla non dipende dal telaio utilizzato per crearla!!!
Allora da cosa dipende???
Per rispondere a questa domanda partiamo da una storia lontana...
|
| Cartagine e la regina Didone |
 "... Giunsero in questi luoghi, ov’or vedrai/ sorger la gran cittade e l’alta rocca/ de la nuova Cartago, che dal fatto/ Birsa no mossi, per l’astuta merce/ che, per fondarla, fèr di tanto sito/ quanto cerchiar di bue potesse in tergo..."
(Eneide: libro 1, 360-368)
La leggenda a cui allude Virgilio è quella secondo cui Didone, arrivata in Africa, chiese al potente Larba, re dei Gentili, un tratto di terra per potervi costruire una città. Il re non volendogliela concedere, le assegnò in segno di scherno tanta terra quanta ne potesse circondare con la pelle di un bue. L’astuta Didone tagliò la pelle in strisce sottilissime e si vide assegnata tutta la terra, affacciata sul mare, che poté circondare con le striscioline attaccate una all’altra. Così costruì Cartagine.
Perché Didone fu astuta?
Sicuramente perché pensò di tagliare la pelle di bue in strisce sottilissime con cui circondare un pezzo di terra. Ma non solo! Didone non disegnò una forma qualsiasi con il cordone che creò, ma disegnò un cerchio (o meglio un semicerchio perché voleva che la città Cartagine si affacciasse sul mare).
I matematici pensano che Didone fosse a conoscenza (una conoscenza empirica, basata sull’esperienza) di una proprietà della circonferenza: la proprietà isoperimetrica, e che la sfruttò a proprio vantaggio.
Iso = uguale quindi isoperimetrico significa di ugual perimetro
Proprietà isoperimetrica del cerchio:
"Fra tutte le figure piane aventi perimetro dato,
il cerchio ha l'area maggiore"
|
| Proprietà isoperimetrica nel piano |
Consideriamo delle figure che hanno lo stesso perimetro; è facile realizzarle: basta prendere come contorno un pezzo di spago e disporlo in vari modi, a quadrato, a triangolo, a cerchio, a...
Come varia l’area fra le figure di ugual perimetro?
Partiamo da un esempio semplice: se, invece di considerare tutte le figure piane, ci si limita a considerare solo i rettangoli, qual è la soluzione del problema?
È facile verificare, attraverso alcuni esempi, che:
- Fra tutti i rettangoli di perimetro fissato, il quadrato è quello di area massima.
Verifichiamolo con GeoGebra 
Questo fatto si può anche esprimere in forma simmetrica:
- Fra tutti i rettangoli di area fissata, il quadrato ha perimetro minimo.
Verifichiamolo con GeoGebra
In generale vale la seguente proprietà:
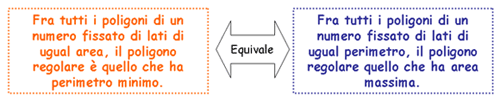
Questo significa che: (ripetere ogni enunciato anche nella forma simmetrica)
- Fra tutti i triangoli di area fissata, il triangolo equilatero è quello che ha il perimetro minimo;
- Fra tutti i quadrilateri di area fissata, il quadrato è quello di perimetro minimo;
- Fra tutti i pentagoni di area fissata, il pentagono regolare è quello di perimetro minimo;
- ...
Abbiamo visto che a parità di area e di numero di lati, i poligoni regolari sono quelli che rendono minimo il perimetro. Ci chiediamo ora:
A parità solo di area, potendo utilizzare un numero qualsiasi di lati, qual’è il poligono con perimetro minimo?
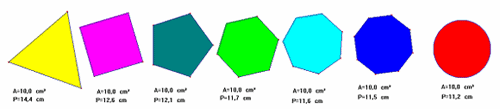
Per quanto osservato precedentemente, possiamo limitarci a considerare solo i poligoni regolari. Con GeoGebra , si può verificare che a parità di area, più lati ha il poligono regolare, meno misura il suo perimetro.
Oppure: a parità di perimetro, più lati ha il poligono più l'area aumenta.
Questo ci conduce intuitivamente al concetto di numero infinito di lati, verso il concetto di approssimazione della circonferenza.
Curiosità:
 La proprietà del cerchio di avere perimetro minimo a parità di area, è stata forse utilizzata nel Medioevo, sempre nella costruzione delle città. Non sono poche infatti le città, di quel periodo, che presentano forma circolare. La ragione era probabilmente, quella di risparmiare sulla lunghezza delle mura di cinta e, nello stesso tempo, di poter sorvegliare meglio gli attacchi dall’esterno.
|
| Proprietà isoperimetrica nello spazio |
Alla luce di quanto detto, possiamo ora rispondere alla questione analoga nello spazio.
Costruire parallelepipedi di ugual volume lavorando con cubi. Si utilizzano 8 cubetti uguali. Si possono costruire 3 parallelepipedi di ugual volume ma con superfici diverse: il primo ha 32 facce, il secondo 28, il terzo 24.
A parità di volume il cubo
ha la superficie minima.
 Costruire solidi di ugual volume lavorando con l’argilla. Abbiamo visto che a parità di volume il cubo presenta la superficie minima fra i parallelepipedi. Ci chiediamo: fra i solidi che hanno lo stesso volume ma forme diverse, qual è quello di superficie minima?
Sempre con l'argilla, costruiamo prima un cubo. Poi per rendere l’argilla "più compatta", comprimiamo il cubo esercitando pressioni orizzontali (si alza) e verticali (si allarga)... continuando così si nota che via via, ad ogni compressione, il solido va "rotondeggiandosi" sempre di più. Si "sente" che si arriverà ad una sfera.
|
| La divina sfera |
Cosi come il cerchio possiede la proprietà isoperimetrica nel piano, la sfera la possiede nello spazio tridimensionale.
|
| Il principio di minimizzazione |
 La domanda iniziale era: perché le bolle hanno forma sferica?
Le bolle seguono il principio fisico di minimizzazione, una legge di "sforzo minimo".
Un comportamento diffusissimo in fisica che spiega perché le palle rotolano giù per un pendio e le molle tendono a ritornare nella loro posizione di equilibro.
In una bolla di sapone la tensione superficiale tende sempre, come per magia, a minimizzare la superficie: per una data quantità di volume d’aria (quello da noi soffiato) la forma con la superficie più piccola è la sfera.
|
|
|
