 |
Capire il mondo attraverso una bolla un percorso di scienze integrate tra schiume e bolle di sapone |
|
|||||||||
| Home | Premessa | Cenni storici | Percorso | Approfondimenti | Fonti | ||||
|
"La ricerca pura si lega da sempre alla più eterea delle realtà. Quello che sembra un gioco da bambini impegna tuttora gli scienziati più creativi, che risolvono problemi senza curarsi troppo delle applicazioni: le quali tuttavia arrivano sempre." Questa frase di Michele Emmer, professore di matematica all’Università "La Sapienza" di Roma, riassume quanto ancora oggi le ricerche sulla natura delle bolle di sapone e delle schiume occupi scienziati di tutto il mondo. Sebbene si sappiano molte cose della schiuma, questa rimane intrisa di misteri e proprietà ancora da spiegare: per esempio, la scorrevolezza della panna montata, una singolare combinazione di caratteristiche solide e liquide, o la cosiddetta sonoluminescenza, un effetto straordinario per cui una bolla che galleggia su un liquido trasforma suono in luce. Gli scienziati affrontano questi argomenti nei numerosi istituti di schiumologia nel mondo con teorie complesse e impressionanti apparecchiature: sonde laser, tecnologia subacquea, sofisticate analisi dei dati e nuovissime tecniche computerizzate. Le molte applicazioni della schiuma migliorano la nostra vita e possono anche salvarla. La schiuma, sotto forma di plastica espansa protegge i serbatoi di carburante delle navette spaziali della NASA e fa da isolante nell’angusto abitacolo dei piloti di Formula 1; metalli espansi servono per costruire protesi più efficaci. In medicina, minuscole bolle iniettate nel flusso sanguigno consentono di diagnosticare un tumore con ultrasuoni; schiume antincendio derivate dalla soia hanno salvato innumerevoli vite durante la seconda guerra mondiale e quelle sviluppate di recente ai Sandia Nazional Laboratories potrebbero attutire l’esplosioni di congegni collocati da terroristi. La scienza della schiuma e delle bolle trova applicazioni in luoghi inaspettati. E' attraverso lo studio delle bolle di sapone che alcuni biologi stanno cercando di studiare le origini della vita. E' una storia iniziata molti secoli fa, e che continua a generare risultati entusiasmanti. Proviamo a ripercorrerne le tappe principali. Isaac Newton (1642 - 1727), nell'Ottica, la cui prima edizione è del 1704, è stato il primo a descrivere in dettaglio il colore che si osserva sulla superficie delle lamine saponate. Antoine Ferdinand Plateau (1801-1883) nel 1873 pubblica il risultato di quindici anni di ricerche: Statistique expérimentale et théorique des liquides soumis aux seules forces moléculaires. In quel libro si pongono molti problemi che riguardano le lamine e le bolle di sapone. Elaborò la moderna teoria delle superfici minime, quelle superfici che minimizzano l'area della superficie rispetto a qualche proprietà; nel caso della bolla di sapone, rispetto al volume d'aria contenuto. Antoine Ferdinand Plateau fu il più autorevole degli schiumologi. Le sue leggi di geometria della schiuma sono tuttora valide. Egli rimase cieco gran parte della propria vita perché durante certe ricerche di ottica, guardò direttamente il Sole. Continuò comunque a studiare la schiuma e le lamine di sapone con l’aiuto di colleghi e amici. Mise a punto una soluzione di sapone, acqua e glicerina con cui otteneva pellicole che duravano anche 18 ore e potevano essere studiate a lungo. Derivò un insieme di leggi che descrivono le schiume attraverso esperienze e osservazione. Una delle cose più stupefacenti che osservò Plateau è che se si soffia con una cannuccia in una soluzione d'acqua saponata gli angoli che le lamine formano sono solo di due tipi: o di 120° o di 109° e 28'. Un risultato che sarà dimostrato solo nel 1976 dalla matematica americana Jean Taylor. Nel 1902 uscì Soap Bubbles and the Forces Which Moulds Them del fisico inglese Charles V. Boys che racconta tre lezioni tenute nel 1889 davanti a un pubblico di giovani ascoltatori alla London Institution. Il motivo centrale del libro è lo sforzo continuo di svelare i più profondi problemi connessi con la natura fisica delle bolle di sapone attraverso semplici esperimenti spiegati nei minimi dettagli. Molti illustri matematici di tutti i tempi si occuparono di problemi di massimo e di minimo: Il più antico problema di massimo esplicitamente formulato che si conosca è contenuto, secondo Cantor, nella proposizione 27 del libro VI degli Elementi di Euclide che in forma geometrica modificata si può così riassumere: "Dato un triangolo ABC, se da un punto D del lato BC si tracciano le parallele ED ad AC, FD ad AB, l’area del parallelogramma AEDF è massima quando D è il punto medio di BC". 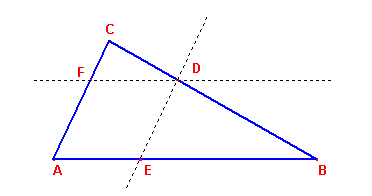 Ne consegue che se AB = AC e l’angolo BAC è retto, allora tra tutti i rettangoli di perimetro dato, il quadrato è quello di area massima; proprietà implicita espressa nella prop 5 del libro II degli Elementi. 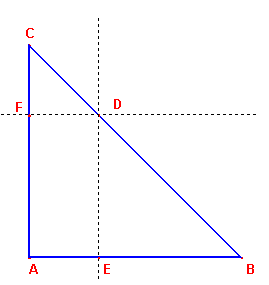 Apollonio (262 a.C- 190 a.C) si occupò, ritenendoli di importante interesse, dei massimi e minimi che si possono condurre da un punto ai punti di una conica. I greci conoscevano già i più celebri problemi di isoperimetria ad esempio:
Zenodoro (200 a.C- 100 d.C) ha raccolto una quantità notevole di teoremi sugli isoperimetri in geometria piana. I suoi risultati sono stati riportati da Pappo che li ha integrati con altri problemi quale ad esempio "fra tutti i segmenti circolari limitati da un arco di data lunghezza il semicerchio ha l’area massima". L’analogo, nello spazio, si trova già in Archimede. Diversi sono stati i matematici che continuarono anche nei secoli successivi ad occuparsi di problemi degli isoperimetri: C. Cramer (1752) ha dimostrato che fra tutti i poligoni piani convessi aventi come lati n segmenti dati, ha area massima quello inscrivibile in un cerchio. S. Lhuilier, ( 1750-1840) ha raccolto, riordinato e ampliato tutto ciò che si conosceva fino a quel tempo sui problemi degli isoperimetri sia nel piano che nello spazio. Fermat (1601-1665) dimostrò che la legge della rifrazione della luce può anche essere enunciata nei termini di un principio di minimo. "In un mezzo non omogeneo, un raggio luminoso che passa da un punto a un altro segue un cammino per cui il tempo impiegato è minimo rispetto a tutti i cammini che congiungono i due punti". Il cammino di minimo tempo è quello per cui gli angoli di incidenza i e di riflessione r sono uguali. 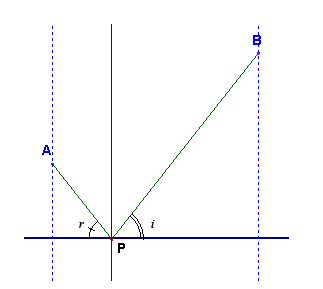 J. Steiner (1796- 1863) ha trattato un notevole numero di questioni di massimo e minimo, utilizzando modi diversi per stabilire le proprietà isoperimetriche del cerchio e della sfera e da queste dedusse numerose applicazioni. Una delle più famose è la seguente: "Tre villaggi A,B,C, devono essere congiunti da un sistema di strade di minima lunghezza totale".  R. Sturm (1803-1885) ha continuato l’opera di raccolta e perfezionamento di Steiner riordinando le questioni di massimo e minimo in un unico libro Maxima und Minima in der elementaren Geometrie - Berlin 1910. Fino ad allora, i problemi venivano affrontati per via sintetica, mettendo in evidenza solo le condizioni necessarie cui la figura doveva soddisfare. La trattazione rigorosa di tutta la teoria degli isoperimetri e delle questioni di massimo e minimo fu realizzata grazie ai metodi dell’Analisi. Fu così possibile ricondurre le ricerche di massimi e minimi delle funzioni di una o più variabili ad un’applicazione sistematica del calcolo delle derivate e fu possibile inoltre risolvere problemi dell’isoperimetria solida. Nella sua tesi di laurea del 1851 Riemann fu criticato e ignorato dai matematici del tempo, in particolare da Weierstrass, su una questione di esistenza di un minimo. Ad esempio, se si considera il problema "dati due punti A e B ad un distanza d su una retta r, determinare la poligonale di minima lunghezza che parta da A in direzione perpendicolare a r e termini in B". 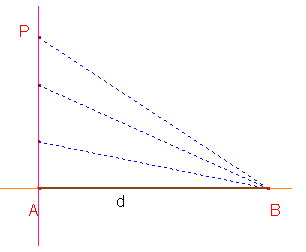 Ancora, nel caso della classe dei numeri 1; 1/2 ; 1/3... l’estremo inferiore è 0, ma non appartiene alla classe, pertanto tale classe non ammette minimo. Furono necessari molti anni di ricerche perché Hilbert (1862_1943) riuscisse a dare una dimostrazione completa e rigorosa della questione irrisolta. Hermann Schwarz (1843-1921) contribuì alla teoria delle funzioni e all’analisi, ma si dedicò anche a questioni elementari quali: "dato un triangolo acutangolo, inscrivere in esso un altro triangolo di perimetro minimo". Egli dimostrò che esiste un solo triangolo e che è quello i cui vertici sono sono i piedi delle altezze. 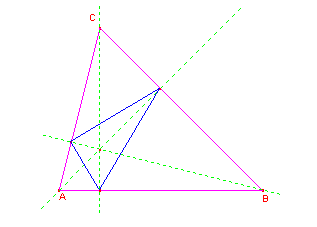 Molti matematici ancora oggi stanno portando avanti ricerche in questo campo per dimostrare proprietà di minimo nella configurazione che formano due o più bolle di sapone se si toccano.  Per approfondire due articoli di Michele Emmer: |