Elenco dei problemi già proposti
(selezionare per vedere i commenti completi):
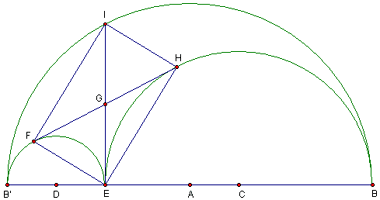
Il grande Archimede trattò la figura sottostante nel suo 'Libro dei Lemmi', chiamandola arbélos (coltello del calzolaio).
Tracciata la semicirconferenza
di diametro BB', si prenda
sullo stesso diametro un punto E, e si traccino, internamente alla
prima, le semicirconferenze di diametri B'E (1)
e EB (2). Si traccino ancora
le tangenti comuni a 1 e
2 e si considerino i punti
E, F, I, H.
Rispondere, motivando, alle seguenti domande:
Di che natura è il quadrilatero EFIH?
Qual è la posizione del punto E che rende massima l'area della regione delimitata dalle tre semicirconferenze?
Trovare una dimostrazione del seguente fatto.
Nella successione 1, 3, 5,
11, 21, 43, ...
in cui i primi due termini sono 1 e 3 e ciascuno dei successivi è la
somma del precedente e del doppio dell'antiprecedente, la somma di due
termini consecutivi qualunque è una potenza di 2.
È 'intuitivo' che se un rettangolo è inscritto in un'ellisse, i lati debbano essere paralleli agli assi dell'ellisse.
a) Dare una dimostrazione che avvalori l'intuizione.
b) Determinare poi il rettangolo di area massima inscritto nell'ellisse di equazione (x/a)^2+(y/b)^2=1.
N.B.: Essendo questa rubrica rivolta agli studenti del triennio in genere, si presume che, nel risolvere i problemi, l'uso del calcolo infinitesimale sia solitamente da escludersi.
Dimostrare che il grafico della funzione a^x, con a>1, ha al più due punti di intersezione con il grafico della sua funzione inversa e determinare la condizione perché i due grafici non si intersechino.
(Suggerimento: si esamini inizialmente l'equazione: a^x = x ).
Si deve costruire un ponte, perpendicolare alle rive di un fiume, per congiungere due paesi, A e B, posti da parti opposte del fiume e a distanze diseguali dalle rive che si suppongono rettilinee nel tratto considerato.
a) Dove deve essere costruito il ponte affinché il percorso da A a B sia minimo?
b) Dove deve essere costruito il ponte affinché A e B siano alla stessa distanza dall'ingresso del ponte rispettivamente a loro più prossimo?
Giustificare le risposte.
Una mongolfiera è osservata in volo
simultaneamente da tre stazioni radar situate ai vertici di un triangolo
equilatero di lato
a .
Le distanze del pallone dalle tre stazioni, prese in ordine intorno al
triangolo, sono date da R1
, R2 , R3 .
Determina l’altezza del pallone dal piano
del triangolo.
Dati i punti A, B e I, costruire
il triangolo che ha vertici A, B e incentro I.
Dire
a) quando il problema è possibile;
b) quante soluzioni ammette.
a) Dimostrare che presi comunque tre vertici di un cubo, il triangolo da essi individuato è rettangolo oppure equilatero.
b) Calcolare la probabilità che tre distinti vertici del cubo, scelti a caso, individuino un triangolo rettangolo.