ProbleMATEMATICAmente 2002-2003

Problema di Ottobre 2002: Soluzioni

Il testo del problema:

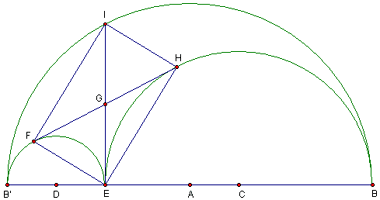
Il grande Archimede trattò la figura sottostante nel suo 'Libro dei Lemmi', chiamandola arbélos (coltello del calzolaio).

Tracciata la semicirconferenza di diametro BB', si prenda sullo stesso diametro un punto E, e si traccino, internamente alla prima, le semicirconferenze di diametri B'E (₁) e EB (₂). Si traccino ancora le tangenti comuni a ₁ e ₂ e si considerino i punti E, F, I, H.
Rispondere, motivando, alle seguenti domande:

• Di che natura è il quadrilatero EFIH?

• Qual è la posizione del punto E che rende massima l'area della regione delimitata dalle tre semicirconferenze?

COMMENTO

Abbiamo ricevuto tre risposte, tutte dall’I.T.C.G. “Ruffini” di Imperia.

• Simone Carli. (V^a A programmatori) ha scelto la via analitica per dimostrare la prima parte del teorema, e la dimostrazione è corretta. Anche la risposta al secondo quesito è corretta. Complimenti a Simone!  Potete vedere il lavoro di Simone in formato Acrobat (PDF) "cliccando" QUI (vedi note in fondo a questa pagina).

• Davide Manetti e Luca Arrigo (V^a A) hanno tentato una dimostrazione per via grafica usando Cabri (scaricate il file per Cabri).
  Anche se incoraggiamo l’uso del software, abbiamo qualche dubbio che esso, da solo, possa “dimostrare” un teorema. Sarebbe bene che Davide e Luca approfondissero quale differenza esiste tra congettura, verifica e dimostrazione.

Entrando nel merito del problema, vorremmo richiamare l’attenzione degli studenti sul fatto che la retta FH è data come tangente a ₁ e ₂, quindi questo fatto va assunto come ipotesi.
Dunque, che la costruzione della tangente comune sia un punto fondamentale per la costruzione della figura è vero; non lo è per la dimostrazione richiesta nel primo quesito.

La classe III^a A programmatori ha svolto un’apprezzabile attività di laboratorio con DERIVE (scaricate il file per Derive), suggerita dalla risoluzione di Simone Carli. Tutti i passaggi di calcolo sono stati puntualmente eseguiti e sono stati verificati i risultati. Il software è servito a confermare la bontà delle risposte date al 1° quesito.

Una nota che ci sentiamo di fare riguarda il sistema di equazioni alle linee 2 e 3 del foglio DERIVE.
Invitiamo gli studenti a porsi le seguenti domande:

• Di che grado è il sistema?
• Quante soluzioni dobbiamo aspettarci?
• Qual è il significato geometrico di tali soluzioni?

Su questi punti anche la riflessione di Simone Carli è stata un po’…sbrigativa!

Nessun problema è mai veramente chiuso!
Invitiamo gli studenti a tentare una risoluzione 'sintetica' del 1° quesito del problema proposto in Ottobre.
Negli archivi del sito di ProbleMATEMATICAmente troverete il testo del problema e la costruzione da giustificare.

AGGIORNAMENTO DELL' ULTIMA ORA:

In ritardo di qualche giorno - dovuto a problemi di funzionamento della posta elettronica connessi con il terremoto che ha colpito Catania - ci è arrivata la soluzione di Daniele Urzì, classe V^a B, Liceo Scientifico “Galileo Galilei” di Catania.
Daniele aggira l'ostacolo insito nell'enunciato dimostrando, prima, che il quadrilatero in questione è un rettangolo, e poi che la retta GH è la tangente in comune alle due semicirconferenze. Potete vedere il lavoro di Daniele in formato Acrobat (PDF) cliccando QUI.
Ci complimentiamo con Daniele, se non altro per avere colto dove si annida la difficoltà della dimostrazione.
Per lo studio del massimo dell’area Daniele propone due modi di procedere; il secondo però è da preferire al primo in quanto, per trovare il massimo, non vengono usate le derivate.

Le risposte ricevute diventano quindi quattro.

AGGIORNAMENTO SUCCESSIVO:

Valerio Gugliotta, III^a A programmatori, ITCG "Ruffini" di Imperia, dimostra per assurdo la tesi, con una dimostrazione molto articolata e ben condotta dal punto di vista logico-formale.