| 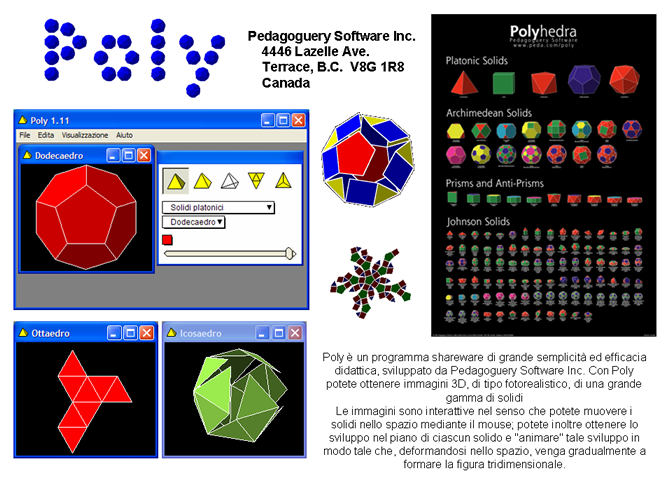
Poly è un programma shareware di
grande semplicità ed efficacia didattica,
sviluppato da Pedagoguery Software Inc.
-
Poly include
tutti i seguenti poliedri:
Solidi platonici
Ogni poliedro platonico è costruito (copie multiple di) un solo poligono
regolare; lo stesso numero di facce poligonali è usato attorno ad ogni
vertice. Un poligono è regolare se tutti i suoi spigoli hanno la stessa
lunghezza e tutti i suoi angoli interni sono uguali.
Solidi Archimedei
I solidi Archimedei furono definiti storicamente da Archimede, anche se
noi abbiamo perso le sue scritture. Tutti i solidi archimedei sono poliedri
uniformi con facce regolari. Un polyhedro con facce poligonali e regolari
è uniforme se ci sono operazioni di simmetria che portano un vertice attraverso
tutti gli altri vertici e nessuno altro punto nello spazio.
Prismi e Anti-Prismi
Dopo i Platonici ed i solidi di Archimede, gli unici poliedri convessi
che rimangono con facce regolari sono prismi ed anti-prismi. Questo fu
mostrato da Johannes Kepler che anche diede i nomi ai solidi Archimedei.
Johnson Solids
Dopo avere preso in considerazione il tre categorie, c’è solamente un
numero limitato di poliedri convesso con facce regolari. L'enumerazione
di questi poliedri fu compiuta da W. Johnson Norman.
Catalan Solids
I solidi catalani sono duali dei solidi di Archimede. Un duplice di un
poliedro è costruito sostituendo ogni faccia con un vertice, ed ogni vertice
con una faccia. Per esempio, il duplice dell'icosaedro è il dodecaedro;
il duplice del dodecaedro è l'icosaedro.
Dipiramidi e deltoedri
Sfere ed emisferi geodetici
|

