L’attività didattica prende avvio dall’analisi dalle conoscenze e dalle idee comuni degli allievi sull’argomento, tramite un test diagnostico preparato dai docenti sotto forma di questionario: i risultati ottenuti creano la situazione di partenza su cui i docenti elaborano le lezioni frontali dialogiche, i laboratori e il materiale didattico e i tempi di esecuzione. Il lavoro prevede di cogliere inizialmente le sollecitazioni e gli esempi che provengono dall’osservazione della realtà.
E’ opportuno che la costruzione di un quadro organico dei concetti geometrici scaturisca da un atteggiamento di ricerca e di osservazione del mondo per individuare le caratteristiche geometriche degli oggetti e i cambiamenti che questi possono subire nello spazio e nel tempo.
Opportuna è anche la realizzazione di attività legate alla manualità (la piegatura della carta o la costruzione di modelli concreti di oggetti…), utilizzando anche materiale cosiddetto “povero”, e l’uso di materiale strutturato (la tela elastica…) che offre la possibilità di realizzare trasformazioni in modo Nelle scuole secondarie si sono diffusi strumenti informatici e pacchetti software per l’insegnamento della geometria che risultano molto facili, intuitivi e particolarmente utili per verificare alcune importanti proprietà geometriche delle trasformazioni geometriche del piano.

La progettazione, in una ottica di tipo costruttivista, prevede

• il coinvolgimento diretto degli allievi
• le attività di gruppo
• la consapevolezza metacognitiva

L’interesse nei confronti dei processi metacognitivi deriva dalla convinzione che chi affronta un problema deve, per trarre il massimo vantaggio dalla sua attività ,essere in qualche modo consapevole della suo processo cognitivo.

• la multimedialità

Le attività multimediali permettono di rispettare alcuni principi basilari della didattica e quindi possono favorire i processi di apprendimento in quanto negli allievi determinano (vedi Gramigna A., Righetti M., Multimedialità e società complessa, Franco Angeli, Milano, 2001):

• Partecipazione
• Immersione
• Inclusione
• e non in ultimo abilità motorie

permettendo

• gradualità dei concetti per facilitare l’apprendimento mediante frazionamento degli obiettivi didattici,
• utilizzo di modalità di insegnamento coinvolgenti e rassicuranti attraverso la presentazione di specifiche situazioni
• l’ appropriarsi di concetti a partire dalla soluzione di problemi concreti

Il tema Simmetrie si presta ad attività operative e laboratoriali per gli studenti, che con la loro partecipazione diretta prestano maggiore attenzione e disponibilità ad accettare nuovi concetti.

Per attuare questo procedimento si propone in ambito matematico l’utilizzo di strumenti tradizionali come la riga e il compasso e di software didattici come Cabri-géomètre. Ognuno di essi presenta una valenza didattica molto forte e l’utilizzo combinato di tutti questi strumenti crea una situazione di notevole coinvolgimento.

Il computer, nel processo di insegnamento-apprendimento degli alunni attrae grazie agli aspetti ludici e stimola dal punto di vista audio-visivo aumentandone la motivazione.
All’aspetto leggero del “gioco” i software didattici aggiungono opportunità di personalizzazione e flessibilità del compito proposto che verrà quindi adeguato alle capacità, rispettando i tempi dell’allievo; prevedono inoltre la creazione di ambienti di apprendimento e di problematiche su cui operare con discussioni e riflessioni, favorendo negli allievi le capacità di congetturare e argomentare, che sono fondamentali per l’introduzione delle dimostrazioni matematiche.

Sottolineiamo l’importanza nel binomio insegnamento-apprendimento della figura dell’insegnante come guida alla scoperta e alla costruzione dei saperi, come mediatore e coordinatore delle attività e delle relazioni, come progettistica dei percorsi educativi.

• il metodo integrato

L’argomento delle simmetrie costituisce un’occasione per affrontare in modo naturale temi scientifici di fisica, chimica e matematica e consente anche agganci con l’architettura, la biologia, l’arte e la musica.

                                  

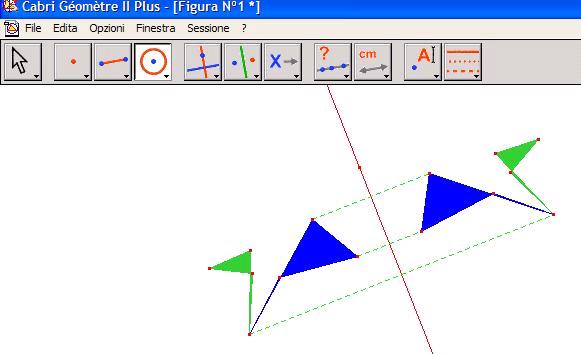
Le attività didattiche si svolgono complessivamente in tre tipi di strutture:

• l'aula didattica: può essere quella della scuola o di un museo, anche improvvisata in un ambiente aperto
• il museo, l’orto botanico: le esposizioni rappresentano il punto di partenza per approfondimenti dialogici in cui si lascia molto spazio alla curiosità dell'utente, saggiandone al tempo stesso l'interesse e la preparazione per meglio calibrare l'intervento
• il lavoro sul campo: si opera in un ambiente o in una ricostruzione di esso (laboratorio di analisi biologica, scavo archeologico, stazione di osservazione della fauna, laboratorio di cristallografia, laboratorio di informatica, percorso in città per cercare regolarità e simmetrie in monumenti cittadini..) in cui l'osservatore diventa egli stesso protagonista.

                                  

• collegamenti storico – epistemologici

Si ritiene che l’approccio storico serva da motivazione, possa chiarire meglio l’argomento e i processi che hanno portato alla introduzione di un concetto, mettendo in grande rilievo come l’opera del matematico sia in divenire e connessa con la risoluzione di problemi.

• Per gli aspetti che riguardano le scienze la metodologia utilizzata è quella chiamata “Lo studio di caso” e consiste nella descrizione dettagliata di una situazione reale.

In questo modo si intende sviluppare negli studenti le capacità analitiche necessarie per affrontare sistematicamente una situazione complessa di cui sono fornite tutte le indicazioni fondamentali. L'obiettivo di questa tecnica non è quello di risolvere un problema, bensì quello di imparare ad affrontare i problemi, ad individuarli e a posizionarli.
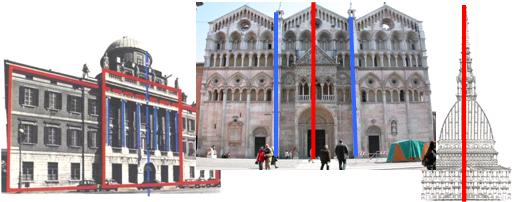
Si comincia con un’attività di laboratorio, (inteso come “spazio mentale attrezzato”) in cui gli studenti disegneranno un animale immaginario, in base ad alcune indicazioni relative ad un ipotetico ambiente di vita, che presenti un grado di simmetria adeguata.
Si procede con l’osservazione delle diverse forme presenti in natura e con la descrizione di alcune situazioni. Segue una discussione di gruppo sulle possibili interpretazioni delle osservazioni fatte. La discussione, moderata dall’insegnante, deve condurre alla relazione fra forma e ambiente, ma anche di molteplicità delle soluzioni adottate per la sopravvivenza e quindi condurre verso i concetti evolutivi di adattamento e di selezione naturale.
Al termine del percorso, si ripeterà l’esperienza introduttiva, per verificare la comprensione della relazione fra forma e ambiente.
Oltre allo sviluppo delle capacità analitiche, l'interazione tra gli studenti permette di capire come uno stesso problema possa essere valutato in modo diverso da persone diverse e mette in evidenza le difficoltà che presenta il pensare ad un problema reale e il giungere ad una eventuale soluzione di gruppo.


Cabri-géomètre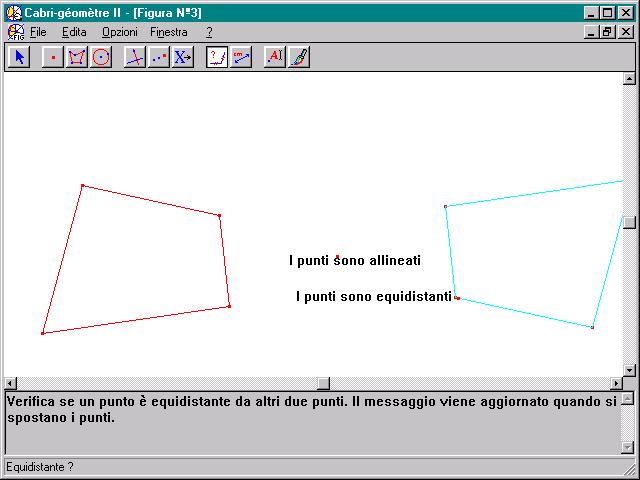

La prima versione di questo software è stata realizzata presso il Laboratoire de Structure Discrete et de Didactique de l’Université “Joseph Fourier” di Grenoble (Francia) nel 1988. Il suo nome è stato ricavato da “CAhier de BRouillon Interactif de Gèomètrie” (Quaderno di appunti interattivo di geometria). Era stato sviluppato come un programma per lo studio dei grafi che permetteva di deformare una configurazione con lo spostamento di uno dei punti base del fascio e si è pensato quindi di utilizzarlo per ottenere un programma che consentisse di realizzare figure geometriche nel piano e di variarle istantaneamente muovendo i punti base della costruzione.
Questo software ha una notevole valenza didattica perché permette di vedere in maniera vivace e dinamica, per le caratteristiche di variabilità delle figure che si possono tracciare, le proprietà delle figure geometriche che invece sono spesso presentate in modo statico all’interno della scuola.
Il programma, inoltre, ben si integra con la trattazione delle trasformazioni geometriche del piano e quindi in particolare con le simmetrie assiali e centrali. Sembra largamente accertato dai docenti che l’introduzione di questo software favorisca un insegnamento ed un apprendimento più dinamico e coinvolgente della geometria. In questo senso ci sono oggi, in Italia e nel mondo, moltissime esperienze di introduzione del Cabri-géomètre nell’insegnamento della geometria a tutti i livelli di scuola.
Grazie alla possibilità di trascinamento dei punti base di una figura è possibile indagare sulle proprietà invarianti di una data configurazione. Le proprietà vengono visualizzate in modo dinamico, con la possibilità di tenere sotto controllo visivo una figura e le sue variazioni. Quali sono i cambiamenti introdotti nella didattica? Il software non fa dimostrazioni ma permette di proporre in laboratorio dei problemi e consente la formazione di congetture che saranno poi sottoposte a verifica: l’approccio alla geometria diventa più intuitivo e si può dare il giusto spazio alla fase dell’esplorazione e della creatività. Risulta più facile “fare matematica“ senza soffermarsi sui particolari formali e sulle difficoltà di calcolo, negli allievi si raggiunge una maggiore comprensione del significato degli “oggetti” matematici che si studiano e nella pratica didattica si può lavorare “per problemi”, evitando la presentazione classica della matematica scolastica, vista come asettica e dogmatica.
L’uso dei software didattici si inserisce in una tradizione consolidata legata all’uso di strumenti mediatori dell’attività di insegnamento – apprendimento: per esempio è ampiamente riconosciuto che l’uso del compasso aiuta nell’evidenziare il ruolo del centro e del raggio nella definizione di circonferenza come luogo geometrico. D’altra parte il loro uso richiede competenze sia di carattere tecnico-operativo sia metodologico da parte del docente, che deve progettare l’azione didattica, suggerire e creare situazioni problematiche, suscitare e coordinare discussioni in classe, creare situazioni di attività cooperative, in piccoli gruppi e aiutare l’allievo nella ricerca di informazioni.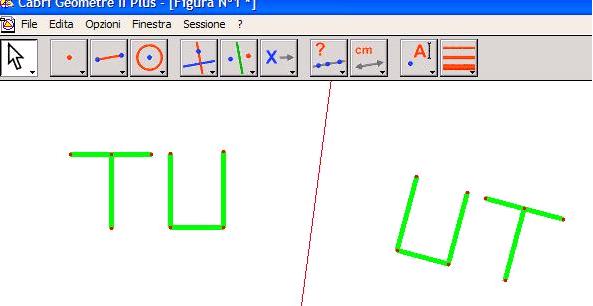

In questo quadro l’uso della tecnologia deve essere visto in relazione all’attività di insegnamento apprendimento nel suo complesso e non solo per lo sviluppo di specifiche attività o per lo svolgimento di specifici compiti. Precisamente deve essere privilegiato un uso a supporto di processi di insegnamento-apprendimento che si realizzano nel lungo periodo per lo sviluppo di conoscenze complesse e articolate come quelle coinvolte nella risoluzione di problemi, nello sviluppo di congetture e dimostrazioni e nelle attività di modellizzazione.
Per quanto riguarda l’uso degli strumenti delle nuove tecnologie da parte degli studenti, ricordiamo lo studio di Rabardel (1995) che rileva una distinzione tra artefatto e strumento: l’artefatto diventa strumento quando lo studente ha imparato ad usare e gestire l’artefatto e sa creare schemi di uso personali e condivisi socialmente. Particolare interesse riveste lo studio di Assude e Gelis (2002) sulle relazioni dialettiche tra nuovi e vecchi strumenti nell’ambito della realtà classe, nei rapporti tra nuovi problemi e attività tradizionali e relativamente ad ambienti di lavoro diversi. Su questa stessa linea sono gli studi di Arzarello et al. (2002), che hanno promosso l’uso di Cabri per attività di esplorazione e scoperta e per la produzione di congetture, verifiche e dimostrazioni.
Di grande interesse è l’analisi di Tomasi (2003) sui problemi della formazione degli insegnanti relativamente al ruolo del docente nell’ambito dell’insegnamento-apprendimento con Cabri.


Arzarello F. et al.(2002), A cognitive analysis of dragging practices in Cabri environments,ZDM 2002,34(3)
Assude T.& Gelis J.M.(2002), La dialectique ancien-vouveau dans l’integration de Cabri-Géomètre a l’ecole primaire, educational Studies in Mathematics
Gramigna A., Righetti M., Multimedialità e società complessa, Franco Angeli, Milano, 2001
Colette Laborde (2004), New technologies as a means of observing students' conceptions and making them develop: the specific case of dynamic geometry, ICME 10
Rabadel P.,(1995), Les hommes e les tecnologies, Armand Colin, Paris
Tomasi L., Cabri in classe e nella rete: visualizzazione dinamica e insegnamento della geometria, in CABRIRRSAE, n. 34-35, giugno 2003.