 |
Capitolo II:
Paragrafo 1
Esercizio 1.1
Esercizio 1.2
Esercizio 1.3
Esercizio 1.4
Esercizio 1.5
Esercizio 1.7
 Download
del Documento Word [CapIIp1.doc, 41K] Download
del Documento Word [CapIIp1.doc, 41K]
Paragrafo 2
Esercizio 2.2
Esercizio 2.3
Esercizio 2.5
 Download
del Documento Word [CapIIp2.doc, 37K] Download
del Documento Word [CapIIp2.doc, 37K]
Paragrafo 3
Esercizio 3.3
 Download
del Documento Word [CapIIp.doc, 19K] Download
del Documento Word [CapIIp.doc, 19K]
Paragrafo 4
Esercizio 4.4
Esercizio 4.9
Esercizio 4.13
Esercizio 4.17
 Download
del Documento Word [CapIIp4.doc, 46K] Download
del Documento Word [CapIIp4.doc, 46K]
Paragrafo 7
Esercizio 7.5
 Download
del Documento Word [CapIIp7.doc, 32K] Download
del Documento Word [CapIIp7.doc, 32K]
Paragrafo 8
Esercizio 8.2
 Download
del Documento Word [CapIIp8.doc, 19K] Download
del Documento Word [CapIIp8.doc, 19K]
Paragrafo 9
Esercizio 9.8
 Download
del Documento Word [CapIIp9.doc, 21K] Download
del Documento Word [CapIIp9.doc, 21K]
Paragrafo 11
Esercizio 11.1
 Download
del Documento Word [CapIIp11.doc, 20K] Download
del Documento Word [CapIIp11.doc, 20K]
Paragrafo 12
Esercizio 12.5
 Download
del Documento Word [CapIIp12.doc, 31K] Download
del Documento Word [CapIIp12.doc, 31K]

Esercizio 1.1
Se f, g sono elementi di A,
l'addizione è definita tramite (f+g): X ->
k: x --> f(x)+g(x). La moltiplicazione
esterna è definita tramite l.f:
X -> k: x -->
l.f(x). La verifica degli assiomi
di k-spazio vettoriale non presenta difficoltà ed è lasciata
al lettore.
Esercizio 1.2
(a), (b): si; (c), (d), (e)
: no. Nel caso (c): (0, 0, 0 ) non appartiene a
E, nel caso (d): (0, 0) non appartiene a
E. Nel caso (e): a = (1, 1) e b = (2, 2) appartengono a
E, ma a-b = (-1, -1) non appartiene a
E. Quindi (E, +) non è un sottogruppo, a fortiori (E,
+, .) non è un k-spazio vettoriale.
Esercizio 1.3
(i), (ii): si; (iii), (iv): no. Nel caso (iii) (A, +)
non è un gruppo. Si può anche osservare che se M =  con ab diverso da 0 allora 2.M non appartiene a
A. Nel caso (iv), 0 non appartiene a A.
con ab diverso da 0 allora 2.M non appartiene a
A. Nel caso (iv), 0 non appartiene a A.
Osservazione:
Identificando M2(R) con R4 tramite
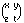 -->
(x, y, z, t) vediamo che A è definito dalle seguenti equazioni:
(i) x = t, y = z, (ii) t = 0, y = x+z, (iii) t = 0, y = xz, (iv) x =
z, t = 1. Nei casi (i), (ii) le equazioni sono lineari omogenee mentre
questo non è vero nei casi (iii) (y = xz non è lineare)
e (iv) (t = 1 non è omogenea) -->
(x, y, z, t) vediamo che A è definito dalle seguenti equazioni:
(i) x = t, y = z, (ii) t = 0, y = x+z, (iii) t = 0, y = xz, (iv) x =
z, t = 1. Nei casi (i), (ii) le equazioni sono lineari omogenee mentre
questo non è vero nei casi (iii) (y = xz non è lineare)
e (iv) (t = 1 non è omogenea)
Esercizio 1.4
(i) (a) Il sottospazio <u, v> generato da
u e v è contenuto nel sottospazio
<x, y> generato da x e y: sia w in
<u, v>, allora w = mu+lv
= (m+l)x+(m-l)y
e quindi w appartiene a <x, y>.
(b)
Adesso mostriamo che <x, y> è contenuto in
<u, v>: dalle ipotesi si ricava: u+v = 2x, u-v = 2y, e
siccome 2 è invertibile in C: x = 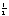 (u+v),
y = (u+v),
y = 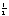 (u-v). Si conclude
come prima. (u-v). Si conclude
come prima.
(ii)
Se k = Z/2Z si ha -1 = 1, quindi u = v e la relazione
precedente non è più vera. Per esempio sia E = k2,
x = (1, 0), y = (0, 1). Allora u = v = (1, 1), e nè x nè
y appartengono a <u>.
Esercizio 1.5
Dimostriamo: F U H è un sottospazio vettoriale
se e solo se F è contenuto in H o H è contenuto in
F.
(<=)
chiaro: se F è contenuto in H allora F U H = H è un sottospazio.
(=>)
Si ragiona per contrapposizione mostrando: F non contenuto in H e H
non contenuto in F => F U
H non è un sottospazio vettoriale.
Se
F non è contenuto in H esiste f in F tale che f non appartiene
a H. Nello stesso modo esiste h in H tale che h non appartiene a F.
Mostriamo che h+f non appartiene a H U F.
Se
h+f appartiene a H allora h+f = h', con h' in H. Pertanto f = h'-h appartiene
a H, ma questo è assurdo. Nello stesso modo si mostra che h+f
non appartiene a F, e la tesi segue.
Esercizio 1.7
(a) E' chiaro che, se i è diverso da k, l'intersezione
di Ei e Ek è uguale a {0}.
Si ha v = 3e1+2e2, v = -e1+2e3,
v = (1/2)e2+(3/2)e3. Visto che e3 =
2e1+e2, si ha E1+E2+E3
= <e1, e2> (ae1+be2+de3
= (a+2d)e1+(b+d)e2).
La somma non è diretta perchè per esempio il vettore v
ammette le due decomposizioni v = 3e1+2e2+0e3
= -e1+0e2+2e3, come somma di elementi
di E1, E2, E3.
(b)
Sia u nell'intersezione di <x,
y> con <z>, allora u = ax+by
e u = lz. Si ricava il sistema: a+b
= 0, a+2b
= 0, 0 = 3l. Da cui l
= 0 e pertanto u = 0. Quindi <x, y> e <z> sono in somma
diretta.
(c)
(i) Osserviamo che <x, y> + <z> = <x> + <y>
+ <z>. Da (b) la prima somma è diretta quindi ogni vettore
di <x> + <y> + <z> si scrive in modo unico come somma
di un vettore in <x, y> e di un vettore in <z>. Siccome
<x> e <y> sono in somma diretta, la scrittura come somma
di un vettore di <x> e di un vettore di <y> è unica.
Concludiamo che la somma <x> + <y> + <z> è
diretta.
(ii)
La somma <x, y> + <z> è diretta: se ax+by
= lz si ricava il sistema: 2a
= l, a+b
= 0, a+3b
= 2l, la cui unica soluzione è
(a, b,
l) = (0, 0, 0). Siccome anche la somma
<x>+<y> è diretta, come prima si conclude che la
somma <x> + <y> + <z> è diretta.

Esercizio 2.2
(a) no: f(0, 0) = (1, 0) diverso da (0, 0); (b) si (cfr
Es.2.1); (c) no: f(l(x, y))
= l(2x-y, lx2+y)
diverso da lf(x, y).
Esercizio 2.3
Le applicazioni f e g sono lineari (cfr Es.2.1).
Abbiamo
Ker(f) = {(x, y)/ 3x-y = 0 e x+y = 0}. Da x+y = 0 viene x = -y, inserendo
nella prima equazione si ricava x = 0, e poi y = 0. Quindi Ker(f) =
{(0, 0}. In particolare f è iniettiva. L' applicazione f sarà
suriettiva se per ogni (u, v) in R2 esiste (x, y)
in R2 tale che f(x,
y) = (u, v) ossia se il sistema: (i) 3x - y = u
(ii) x+y = v ammette una soluzione per ogni (u, v). Sommando le due
equazioni viene u+v = 4x da cui x = (u+v)/4. Inserendo in (ii): y =
(3v-u)/4. Quindi f è suriettiva e Im(f) = R2.
Finalmente f è biiettiva perchè iniettiva e suriettiva.
Abbiamo
Ker(g) = {(x, y) / 2x-y = 0 e 4x - 2y = 0}. Le due equazioni sono proporzionali
e risolvendo il sistema otteniamo: Ker(g) = {(x, 2x) / x appartiene
a R}. In altri termini Ker(g)
è il sottospazio generato dal vettore (1, 2); in particolare
g non è iniettiva. L'applicazione g non è suriettiva.
Infatti il sistema: (i) 2x-y = u (ii) 4x-2y = v ammette una soluzione
se e solo se v = 2u. Questa condizione è chiaramente
necessaria e se è soddisfatta allora, per esempio, g(0, -u) =
(u, 2u). Quindi Im(g) = {(u, 2u) / u appartiene a R}.
Esercizio 2.5
Iniziamo col mostrare che (F, +) è un gruppo abeliano.
Chiaramente la legge + su F è interna e commutativa. Essendo
f biiettiva esiste un unico elemento di F, chiamiamolo 0, tale che f-1(0)
= 0 (= il vettore nullo di E). In particolare f(0) = 0. Mostriamo che
0 è l'elemento neutro. Per ogni x in F: x + 0 := f(f-1(x)+f-1(0))
= f(f-1(x)+0) = f(f-1(x)) = x. Mostriamo che ogni
elemento x di F ha un simmetrico. Sia u = -f-1(x). Siccome
f è biiettiva esiste un unico elemento, -x, di F tale che f-1(-x)
= u. Abbiamo x+(-x) = f(f-1(x)+f-1(u)) = f(f-1(x)-f-1(x))
= f(0) = 0. Verifichiamo adesso l'associatività: (x+y)+z = x+(y+z).
Abbiamo (x+y)+z = f(f-1(x+y)+f-1(z)). Osserviamo
che x+y = f(f-1(x)+f-1(y)). Pertanto f-1(x+y)
= f-1(f[f-1(x)+f-1(y)]) = f-1(x)+f-1(y).
In conclusione: (x+y)+z = f[(f-1(x)+f-1(y))+f-1(z)].
Nello stesso modo x+(y+z) = f[f-1(x)+(f-1(y)+f-1(z))].
L'addizione in E essendo associativa concludiamo che (x+y)+z = x+(y+z).
Questo dimostra che (F, +) è un gruppo abeliano. Inoltre se u,
v sono elementi di E ponendo x = f(u), y = f(v) abbiamo, per definizione:
x+y = f(f-1(x)+f-1(y)) = f(u+v), ossia f(u+v)
= f(u)+f(v) e quindi f è un morfismo di gruppi da (E,+) in (F,+).
Mostriamo
che " (l,
m) e k2,
" x e
F: (l+m)x
= lx+mx.
Per
definizione: (l+m)x
= f[(l+m)f-1(x)]
= f[lf-1(x)+mf-1(x)]
(perchè E è uno spazio vettoriale) = f(lf-1(x))+f(mf-1(x))
(perchè f è un morfismo dei gruppi additivi) = lx
+ mx (per definizione).
Nello
stesso modo: " l
e k, "
(x, y) e F2: l(x+y)
= lx+ly.
Infatti l(x+y) = f(lf-1(x+y)).
Abbiamo già visto che f-1(x+y) = f-1(x)+f-1(y)
(cfr anche Es.I.5.9), quindi
l(x+y)
= f[l(f-1(x)+f-1(y))]
= f[lf-1(x)+lf-1(y)]
= f(lf-1(x)) + f(lf-1(y))
= lx+ly.
Osserviamo
che f-1(mx) = mf-1(x).
Infatti, per definizione: mx = f(mf-1(x)).
Detto ciò vediamo che "
(l, m)
e k2, "
x e F: (lm)x
= l(mx).
Per definizione (lm)x = f[(lm)f-1(x)]
= f[l(mf-1(x))]
(perchè E è uno spazio vettoriale) = f[l(f-1(mx))]
(per l'osservazione precedente) = l(mx)
(per definizione).
Finalmente
" x e
F: 1x = x perchè 1x = f(1f-1(x)) = f(f-1(x))
= x. Questo conclude la dimostrazione del fatto che l'addizione e la
moltiplicazione esterna indotte da f conferiscono a F una struttura
di k-spazio vettoriale. Per vedere che f è un'applicazione lineare
rimane da vedere che f(lu) = lf(u)
(abbiamo già visto che f è un morfismo dei gruppi additivi).
Sia x = f(u). Per definizione lx =
f(lf-1(x)) = f(lu);
ossia lf(u) = f(lu).
Siccome f è biiettiva per ipotesi, f è un isomorfismo
lineare.

Esercizio 3.3
Siano e1, ..., en
dei vettori di E che generano E. Sia u e
F. Siccome f è suriettiva, esiste x in E tale che f(x)
= u. Per ipotesi x = Sliei.
Quindi u = f(x) = f(Sliei)
= Slif(ei) (l'ultima
uguaglianza è vera per la linearità di f). Vediamo che
ogni vettore di F è combinazione lineare dei vettori f(e1),
..., f(en), quindi F è finitamente generato.

Esercizio 4.4
Sia z = a + ib un numero complesso
(a, b sono numero reali e i2
= -1). Siccome z = a.1 + i.b, vediamo che ogni numero complesso è
combinazione lineare a coefficienti in R di 1 e di i; quindi
1 e i generano C come R-spazio vettoriale. Essendo la
scrittura z = a.1 + i.b unica, (1, i) è una base di C
come R-spazio vettoriale (in altri termini: se a.1 + i.b = 0
allora a = b = 0, quindi 1 e i sono linearmente indipendenti su R).
Esercizio 4.9
(i) Sia f: R3
--> R2
: (x, y, z) --> (x+y+z, 2x-z). L'applicazione f è lineare
(cf II.§2 Esercizio 2.1). Abbiamo F = Ker(f), quindi F è
un sottospazio lineare (II.§2, Prop. 6).
N.B. Con lo stesso ragionamento,
ogni sottinsieme definito da equazioni lineari omogenee è un
sottospazio vettoriale.
(ii) Cerchiamo una base di
F. Gli elementi di F sono soluzioni del sistema x+y+z = 0, 2x-z = 0.
Dalla seconda equazione si ricava z = 2x, inserendo nella prima: y =
-3x. Quindi F = {(x, y, z) / z = 2x e y = -3x} = {(x, -3x, 2x) / x appartiene
a R} = {x.(1, -3, 2) / appartiene a R} = <(1, -3, 2)>.
Concludiamo che il vettore u = (1, -3, 2) è una base di F (genera
ed è linearmente indipendente). Quindi dim(F) = 1 e un supplementare
di F avrà dimensione due.
Per trovare un supplementare
di F basta per esempio trovare due vettori v, w della base canonica
tali che u, v, w siano linearmente indipendenti; il supplementare sarà
<v, w>. Si verifica facilmente che, per esempio, v = (1, 0, 0),
w = (0, 1, 0) vanno bene.
Esercizio 4.13
Se x appartiene a E allora
x = h + f (in modo unico) con h in H, f in F. Adesso h = Saihi,
f = Sbjfj,
quindi x è combinazione lineare di h1,
..., hk, f1,
..., fn; cioè
h1, ..., hk,
f1, ..., fn
generano E.
Rimane da vedere che i vettori
h1, ..., hk,
f1, ..., fn
sono linearmente indipendenti:
sia Saihi
+ Sbjfj
= 0 una combinazione lineare nulla. Abbiamo Saihi
= - Sbjfj;
cioè h = f, con h = Saihi
in H e f = - Sbjfj
in F.
Il vettore h (= f) appartiene
quindi a l'intersezione di F con H (appartiene sia a H che a F), siccome
F e H sono in somma diretta, la loro intersezione è uguale a
{0}. Quindi h = f = 0.
Da 0 = h = Saihi
segue: ai
= 0 per ogni i (perchè gli hi
sono linearmente indipendenti). Da 0 = f = Sbjfj
segue: bj
= 0 per ogni j (perchè gli fj
sono linearmente indipendenti).
Pertanto h1,
..., hk, f1,
..., fn sono linearmente
indipendenti.
Esercizio 4.17
(i) Abbiamo E = k2
con k il campo F2.
La dimensione di E è 2, una base è, per esempio: e1
= (1, 0), e2 = (0,
1) ("base canonica"). N.B.: questo è vero per un campo
k qualsiasi.
(ii) Abbiamo card(E) = 4; i
quattro vettori di E sono: (0, 0), (1, 0), (0,1), (1, 1)
(iii) Abbiamo già visto
che e1 e e2
sono linearmente indipendenti. E' chiaro che w = (1, 1) e e1
(risp. e2) sono linearmente
indipendenti (anche perchè l'unico scalare non nullo è
1).
(iv) Ci sono 5 sottospazi di
E: {0}, E, <e1>,
<e2>, <w>
(v) Ci sono due supplementari
di F = <(1, 0)>, uno è <e2>,
l'altro è <w>. In particolare F non ammette un'infinità
di supplementari, questo è dovuto al fatto che il campo k è
finito. Se k è infinito, si può dimostrare che ogni sottospazio
proprio ammette un'infinità di supplementari (cf II. §5,
Esercizio 5.2)

Esercizio 7.5
(i) f non suriettiva =>
esiste una forma lineare non nulla j tale
che j°f = 0
Se f non è suriettiva,
dim(Im(f)) < dim(F) e quindi esiste un iperpiano, H, di F contenente
Im(f) (prendere una base di Im(f): v1,
..., vp; completarla
a una base di F: v1,
..., vp, ep+1,
..., en; allora,
per esempio, l'iperpiano < v1,
..., vp; ep+1,
..., en-1> contiene
Im(f)). Abbiamo H = Ker(j) per qualche
forma lineare j (Prop. 9). Siccome
Im(f) è contenuto in Ker(j),
abbiamo j°f = 0.
esiste una forma lineare non
nulla j tale che j°f
= 0 => f non suriettiva
Sia H = Ker(j),
H è un iperpiano. Dalla relazione j°f
= 0, segue Im(f) contenuto in Ker(j)
= H, quindi Im(f) è un sottospazio proprio di F e pertanto f
non è suriettiva.
(ii) Più generalmente
se dim(Im(f)) = dim(F) - r, allora Im(f) è un sottospazio di
codimensione r in F; un tale sottospazio è definito da r equazioni
linearmente indipendenti (cf II.§7, 17), j1,
..., jr;
cioè Im(f) è l'intersezione degli iperpiani Hi
= Ker(ji),
in particolare Im(f) è contenuto in ogni Hi,
quindi ji°f
= 0, per ogni i.

Esercizio 8.2
Tutti i polinomi in questione
hanno grado al più tre, sono quindi elementi dell' R spazio
vettoriale R[X]3.
Siccome dim(R[X] 3)
= 4 (una base è: 1, X, X2,X3),
i cinque polinomi P1,
..., P5 sono linearmente
dipendenti.

Esercizio 9.8
Facciamo direttamente il caso
generale.
Se f: E --> E: v -->
lv è un'omotetia, allora chiaramente
f commuta con ogni endomorfismo g (g(f(v)) = g(lv)
= lg(v) = f(g(v))). Mostriamo che
le omotetie sono gli unici endomorfismi che commutano con ogni altro
endomorfismo.
Sia f un endomorfismo tale
che esista un vettore x con f(x) = v, x e v linearmente indipendenti.
Possiamo completare x, v a una base di E. Siccome un endomorfismo è
definito dai suoi valori su i vettori di una base, esiste un endomorfismo
g tale che g(v) = g(x) = x. Abbiamo g(f(x)) = g(v) = x, mentre f(g(x))
= f(x) = v, quindi f e g non commutano.
Quindi una condizione necessaria
affinchè f commuti con ogni altro endomorfismo è: per
ogni vettore x in E, x e f(x) sono linearmente dipendenti. Mostriamo
che questa condizione implica che f è un'omotetia.
Sia e1,
e2, ..., en
una base di E. Per ipotesi, per ogni i, f(ei)
= liei
. Dobbiamo mostrare che i li
sono tutti uguali. Abbiamo anche f(e1
+ ... + en)
= b(e1
+ ... + en ) (#).
Ma f(e1 + ... + en)
= f(e1) + ... + f(en)
= l1e1
+ ... + lnen.
Confrontando con (#), viene: (b-l1)e1
+ ... + (b-ln)en
= 0. Siccome gli ei
sono linearmente indipendenti segue che: b
= l1
= ... =ln;
quindi f è l'omotetia di rapporto b.
In conclusione se f commuta
con ogni altro endomorfismo allora f è un'omotetia.

Esercizio 11.1
(i) Siccome dim(R3)
= 3, basta mostrare che i tre vettori sono linearmente indipendenti.
Sia av1
+ bv2
+ dv3
= 0 una combinazione lineare nulla. Abbiamo il sistema:
-a
-b + 2d = 0
b
= 0
a
= 0.
Chiaramente l'unica soluzione
è (a, b, d) = (0, 0, 0); quindi
i vettori sono linearmente indipendenti e B' è una base.
(ii) Per determinare mat(f,
B', B'), dobbiamo esprimere f(v1)
(risp. f(v2), f(v3))
come combinazione lineare dei vi.
Sappiamo che f(e1)
= 2v3, f(e2)
= v2, f(e3)
= -v1 + v3.
Abbiamo f(v1)
= f(-e1 + e3)
= -2v3 -v1
+ v3 = -v1
-v3; f(v2)
= f(-e1 + e2)
= -2v3 + v2;
f(v3) = f(2e1)
=
4v3.
-1 0 0
In conclusione, mat(f, B', B') = 0 1 0
-1 -2 4

Esercizio 12.5
(i) E' chiaro che 0 appartiene
a A(g) e che, se f, f' appartengono a A(g), allora, per ogni l,
m, lf
+ mf' appartiene a A(g) (perchè
(lf + mf')°g
= l (f°g)
+ m(f'°g)),
quindi A(g) è un sottospazio vettoriale di End(E). Nello stesso
modo B(g) è un sottospazio vettoriale di End(E).
(ii) Abbiamo: f appartiene
a A(g) se e solo se Im(g) è contenuto in Ker(f). Sia e1,
..., er uuna base
di Im(g) che completiamo a una base di E: B = (e1,
..., er, er+1,
..., en.). Vediamo
che f appartiene a A(g) se e solo se f(e1)
= ... = f(er) = 0,
per il resto f(er+1),
..., f(en) possono
essere qualsiasi.
|
