Intorno al 600 a.C., un uomo di nome Talete di Mileto, inventò ciò che chiamiamo “scienza”.

Prima di Talete, gli studiosi, invece di cercare i principi celati dietro gli eventi insoliti che la natura poneva loro di fronte, ritenevano che la natura operasse in seguito alle vicende fantastiche di personaggi ultraterreni, gli Dei.
In particolare, Talete introdusse l’astrazione in geometria, ossia in quella disciplina che fino ad allora era stata studiata per misurare (metrein) la terra (geo) ed in cui le figure erano oggetti particolari, come recinti o campi. Egli invece concepì la geometria come un’attività puramente speculativa, cosicché analizzando le regole pratiche e le formule empiriche tramandate da Egizi e Babilonesi, vi scoprì un ordine, ossia notò che alcuni fatti geometrici erano deducibili a partire da altri.

Le teorie scientifiche di Talete diedero l’avvio allo studio, da parte degli antichi greci, della matematica come chiave di lettura della natura, cosicché, già nel V secolo a.C., i matematici avevano elaborato lunghe serie di teoremi geometrici in cui ogni teorema veniva dedotto, in modo non formale, da quelli precedenti.

La prima costruzione dei cinque poliedri è dovuta, quasi sicuramente alla scuola Pitagorica. Lo storico Proclo (410 - 485 d.C) nel suo Commento al primo libro degli Elementi di Euclide, meglio conosciuto come Riassunto, osserva che "Pitagora trasformò questo studio in una forma di insegnamento liberale, investigando dall'alto i suoi principi, e, indagando i teoremi astrattamente e intellettualmente, egli scoprì il fatto degli irrazionali e la costruzione delle figure cosmiche (i poliedri regolari)." E’ nel dialogo di Platone che si trova la prima descrizione giunta sino a noi dei cinque solidi regolari, noti per questo motivo anche con il nome di solidi Platonici.

Dal punto di vista storico sembra che solo tre dei cinque solidi regolari siano dovuti a Pitagora e alla sua scuola (VI sec. a.C.); sarebbe stato il matematico Teeteto, contemporaneo di Platone (IV sec. a.C.), a scoprire gli altri due, probabilmente l'ottaedro e l'icosaedro. Inoltre sembra che Teeteto sia stato il primo a scrivere un trattato sistematico sui cinque solidi regolari, ma l'opera è comunque andata persa. Una delle prime opere in nostro possesso in cui, oltre a molte altre nozio¬ni di matematica, si discorre sui cinque poliedri regolari è il "Timeo" di Platone. In questo dialogo il "demiurgo", il Dio di Platone, nella sua opera di generazione dell'universo, modella da uno "sostrato" visibile e in moto disordinato i quattro elementi: aria, acqua, terra e fuoco; e da questi tutte le altre cose.

Platone descrive quindi i cinque poliedri regolari e le loro proprietà; quindi li assume come forme dei quattro elementi. Quindi parlando del "tetragono equilatero" lo associa al fuoco perchè: "di tutte queste forme, quella che ha il minor numero di basi è necessariamente la più mobile per natura, perché è la più tagliente e in ogni sua parte la più acuta di tutte, ed è anche la più leggera". Platone associa poi l'ottaedro all'aria e l'icosaedro all'acqua. Va sottolineato da un lato quanto sia suggestiva l'associazione proposta da Platone, dall'altro il fatto che Platone vede un legame quasi necessario fra le forme geometriche "perfette" e la natura: "perciò conserviamo la verosimiglianza, attribuendo questa forma [il cubo] alla terra, e poi all'acqua la forma meno mobile delle altre, al fuoco la più mobile, e all'aria l'intermedia: e così il corpo più piccolo al fuoco, il più grande all'acqua, e l'intermedio all'aria, ed inoltre il più acuto al fuoco, il secondo per acutezza all'aria, il terzo all'acqua".

Per quanto riguarda il quinto solido regolare, il dodecaedro, nell'Epinomide, sembra che Platone lo identifichi con il quinto elemento, l'etere. Infatti troviamo scritto: "com'è giusto, bisogna parlare anche di cinque corpi solidi, da cui si possono plasmare le più belle e le più perfette figure" e inoltre: "se cinque sono, dunque, i corpi, bisogna dire ch'essi sono il fuoco, l'acqua, e terza l'aria, quarta la terra, quinto l'etere, e che in questi cinque domìni si formano, numerosi e vari, i singoli esseri viventi".
Nel Timeo invece, si nega che l'etere sia un elemento, perchè non è altro che la parte più pura dell'aria; Platone parla invece del dodecaedro in questi termini: "restava una quinta combinazione, e Dio se ne giovò per decorare l'universo".

Nella storia dei poliedri non si hanno nuovi risultati per lungo tempo; sino alla riscoperta della matematica greca ed in particolare degli Elementi di Euclide (323-285 a.C.) alla fine del Medio Evo.

Lo sviluppo assiomatico degli Elementi di Euclide

Il nome di Euclide (circa 300 a.C.) è associato alla sua opera più famosa, gli Elementi, opera che, per la sua diffusione, sia nella lingua originale che in varie traduzioni, segue a ruota soltanto l’Antico e Nuovo Testamento e, forse, la Divina Commedia.
L’opera è divisa in 13 libri e i Libri XI, XII e XIII riguardano proposizioni di geometria solida; in particolare l’ultimo libro è dedicato interamente alle proprietà dei cinque poliedri regolari e termina con una proposizione (Prop.18) in cui si dimostra che non vi possono essere poliedri regolari oltre questi cinque. Quasi 1900 anni più tardi l’astronomo Keplero rimase talmente colpito da questa circostanza che costruì tutta una cosmologia su di essi, ritenendo che tali poliedri avessero “ispirato” il Creatore per la costruzione dell’universo.

L'importanza che Platone dava alla Geometria e alle scienze esatte è sintetizzata dalla scritta che campeggiava all’ingresso della sua Scuola " Nessuno digiuno di Geometria varchi queste porte". Lo stesso Platone , nel Timeo, dice a proposito dei poliedri regolari o platonici, "non accorderemo a nessuno che vi siano corpi visibili più belli di questi".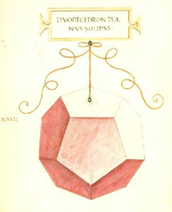

E' abbastanza naturale che, nel Rinascimento, in piena riscoperta della filosofia platonica questi poliedri abbiano goduto di grande popolarità presso gli artisti dell’epoca, tanto è vero che da quel momento risulta difficile distinguere la storia artistica e quella scientifica dei poliedri. I più importanti libri rinascimentali sulla teoria e pratica della prospettiva sono spesso delle sequenze di solidi nello spazio visti sotto diverse angolature.

Dopo Euclide, Archimede si occupa dei poliedri, ma non di quelli strettamente regolari. Egli richiede che:
• le facce siano dei poligoni regolari, anche diversi tra loro ( ad esempio: triangoli equilateri, quadrati).
• le facce poligonali devono essere disposte nello stesso modo intorno ad un vertice.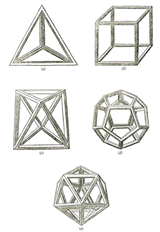
Si parla in tal caso di poliedri semiregolari o Archimedei. Anche per questi solidi c'è un numero limitato di possibilità: in tutto 13.
Anche Apollonio si occupa di poliedri. Si attribuisce a lui una proprietà relativa al dodecaedro e all'icosaedro inscritti nella stessa sfera, proprietà sfuggita ad Euclide. Dobbiamo anche tenere conto del fatto che non avevano la possibilità di scrivere le formule in modo così "compatto": infatti non era nata ancora l'algebra e tutto veniva raccontato in modo discorsivo, (come se si dovesse eseguire un tema).

Nel II sec. d.C. in tutto il mondo greco-romano si accentuano gli atteggiamenti irrazionali, proliferano la magia, l'astrologia, e l'alchimia. Troviamo i poliedri regolari come simboli per gli elementi sotto i quali si può presentare la materia.
Gli alchimisti parlano oltre che di terra (cubo), fuoco (tetraedro), acqua (icosaedro), aria (ottaedro) anche di Quintessenza (etere) simboleggiata da dodecaedro che trova così anch'esso una giusta collocazione.

Verso il III sec. dopo C. c'è una rinascita della matematica con gli studi di Pappo e di Diofanto. Pappo affronta il problema dei poliedri inscritti in una sfera in modo nuovo cioè attraverso la ricerca delle sezioni circolari. Alcuni autori contemporanei di Proclo scrivono un XV libro degli Elementi in cui compare il calcolo del numero dei vertici, degli spigoli e delle facce dei cinque solidi regolari.

Nel XV° secolo con il Rinascimento, dopo un periodo di stallo, troviamo condizioni che favoriscono la ripresa degli studi in campo geometrico. L'arte si avvicina ad un metodo scientifico e usa come strumenti di osservazione la geometria, l'ottica, la teoria della luce e dei colori, l'anatomia e la fisiologia. (Leonardo è un esempio di questo modo di lavorare).
Con la caduta dell'Impero Romano di Oriente, nel 1453 giungono in Italia molti studiosi bizantini portando con sé testi antichi. Nel 1505 viene pubblicata a Venezia una traduzione degli " Elementi " di Euclide e le " Coniche " di Apollonio. La vera molla per riprendere gli studi geometrici sono gli artisti attraverso la formulazione delle regole per la prospettiva centrale e della teoria delle ombre: studi che condurranno alla Geometria Proiettiva.

Furono soprattutto Piero della Francesca tra il 1482 e il 1492 nel suo De quinque Corporibus regolaribus e il suo allievo, il frate matematico ( e forse plagiatore) Luca Pacioli (1445-1514) nel suo De divina proportione a stendere le basi teoriche della prospettiva mentre si deve a Paolo Uccello (Mosaici di S.Marco a Venezia), a Leonardo , che probabilmente fornì l’iconografia per il trattato di Pacioli, ad Albrecht Dürer , oltre che allo stesso Piero, l’applicazione di quei principi nelle loro immortali creazioni artistiche.

La regolarità e bellezza dei solidi platonici non lasciò insensibile neanche il grande astronomo e matematico Keplero (1571 - 1630), che , oltre a scoprire la nuova serie dei solidi stellati, come il dodecaedro che porta il suo nome e sulle cui facce è costruita una piramide regolare, propose un modello del sistema solare basato sui solidi platonici: benchè rivelatosi errato, questo modello è comunque "il risultato di complessi calcoli, ben dettagliato e provocante", secondo la descrizione che ne fornisce lo scrittore A. Koestler.

Ritroviamo quindi i poliedri con Keplero che abbraccia la teoria eliocentrica e si impegna a rafforzarla. Secondo Keplero l'universo è ordinato secondo un piano matematico ed egli ricerca le leggi matematiche nei moti dei pianeti. Nell'opera giovanile "Misterium cosmograficum" Keplero afferma che Dio nel creare l'universo tenne presenti i cinque poliedri regolari egli perciò fissa , in accordo con le dimensioni di tali poliedri, il numero dei cieli, le loro proporzioni e le relazioni tra i loro movimenti.

Keplero cerca di mettere in relazione il raggio dell'orbita intorno al sole di ciascun pianeta con lo spigolo di uno dei cinque poliedri regolari. Realizza così un modello di sistema solare eliocentrico molto particolare, in cui i pianeti descrivono orbite circolari e le sfere generate dalla rotazione di queste sono inscritte o circoscrivono i cinque solidi regolari.
Inoltre Keplero riprende il significato che l'astrologia attribuisce a ciascun pianeta e lo mette in corrispondenza con le caratteristiche dei poliedri. Ad esempio, nel suo modello, tra l'icosaedro e l'ottaedro si trova Venere: questi due solidi sono i meno stabili e rappresentano bene, secondo Keplero, le caratteristiche della femminilità, instabilità e volubilità. ( Si può anche non essere d'accordo!) Mercurio veloce viene accostato all'ottaedro che ruota come una trottola intorno ad un suo asse.
Più tardi Keplero si accorge che il suo modello non corrisponde ai risultati dell'osservazione ed è costretto ad abbandonare le sue ipotesi: che lezione per tanti nostri politici che perseguono la loro strada nonostante l'evidenza di errori alla base della loro teoria, e spesso le loro idee non sono poi neppure così "armoniose" come quelle del grande scienziato!
In realtà calcolando le distanze dei pianeti dal sole d'accordo con il modello di Keplero, si può trovare che tali distanze differiscono da quelle reali con errori fino al 40%.

Verso una nuova geometria.
Lo studio della geometria classica prende in esame le proprietà metriche delle figure cioè le misure di angoli e di lati che restano invariate se la figura stessa viene sottoposta a movimenti rigidi cioè traslazioni, rotazioni e ribaltamenti. Sottoponendo le figure ad un diverso tipo di trasformazione si giunge ad una nuova geometria.
E' quello che è accaduto a partire dal '500 con la teoria della prospettiva. Il problema di quali siano le proprietà geometriche della figura reale che si conservano passando alla sua immagine mediante proiezione, viene sollevato per la prima volta la Leon Battista Alberti. Ad esempio nella prospettiva due linee che nella realtà sono parallele vengono rappresentate in modo da incontrarsi in un punto, le lunghezze e gli angoli perciò si alterano.

Nel '600 prendono avvio i primi studi di geometria proiettiva ad opera di Desargues e Pascal. Un concetto curioso ed importante nella geometria proiettiva è il principio di dualità.
Consideriamo i due assiomi relativi al piano proiettivo:
1. Due punti distinti determinano una ed una sola retta.
2. Due rette distinte determinano uno ed un solo punto.
Ebbene, partendo dal primo assioma è possibile ottenere il secondo scambiando fra loro i termini punto e retta e viceversa.
Questo accade per tutti i teoremi della geometria proiettiva e si dice che punto e retta sono elementi duali.
Così due figure sono duali tra loro quando una è ottenibile dall'altra sostituendo ad ogni elemento l'elemento duale. Anche per la geometria proiettiva nello spazio vale il principio di dualità.
Tale principio applicato ai poliedri fa corrispondere facce a vertici ed implica così che da ogni poliedro possiamo ottenere il suo poliedro duale scambiando fra di loro il numero delle facce con il numero dei vertici e lasciando inalterato il numero degli spigoli.
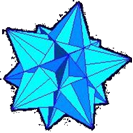
I poliedri regolari non convessi sono quattro. Due di essi, i così detti poliedri di Keplero hanno come facce poligoni regolari stellati; altri due, i così detti poliedri di Poinsot, dal nome del matematico francese Louis Poinsot, (1777 - 1859): sono costruiti in modo che le facce possano interpenetrarsi.
Sono poliedri di Keplero:
Il piccolo dodecaedro stellato che ha come facce 12 pentagoni stellati, ha 12 vertici e 30 spigoli
Il grande dodecaedro stellato che ha ancora come facce 12 pentagoni stellati, ha 20 vertici e 30 spigoli
Sono poliedri di Poinsot
il grande dodecaedro che ha 12 facce a forma di pentagoni regolari, ha 12 vertici e 30 spigoli;
il grande icosaedro ha che ha 20 facce a forma di triangoli equilateri, ha 12 vertici e 30 spigoli

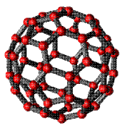
Recentemente uno di essi, l’icosaedro troncato formato da esagoni e pentagoni è assurto a grande popolarità in campo scientifico per la scoperta di una molecola , il fullerene C60, terza forma allotropica del carbonio, costituito da 60 atomi di carbonio che formano esagoni e pentagoni uniti tra loro, con una struttura che ricorda un pallone da calcio.