RAPPRESENTARE IN ASSONOMETRIA CAVALIERA UN TETRAEDRO REGOLARE CON CABRI II

Si deve procedere inizialmente come per il cubo.

Aprire il file in cui è stata memorizzata la macro omologia affine
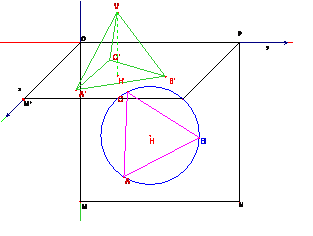
Costruire il riferimento Oxyz , il parallelogramma OM’N’P immagine del quadrato OMNP.
Disegnare una circonferenza e il triangolo equilatero ABC con lo strumento <poligono regolare>
Determinare il triangolo A’B’C’, corrispondente di ABC nella omologia affine di asse y ed avente come corrispondenti i punti M e M’

Disegnare il centro H del triangolo ABC e determinare il corrispondente H’ nell’omologia affine
Occorre ora definire l’altezza del tetraedro. Tale segmento corrisponde al cateto maggiore di un triangolo rettangolo che ha per ipotenusa uno spigolo, cioè il lato del triangolo ABC e per cateto minore il segmento HA che, essendo H il baricentro del triangolo, corrisponderà a 2/3 del lato AB

Usare il comando <calcolatrice> per determinare HA . In figura la variabile a indica la lunghezza dello spigolo del tetraedro.

Con < trasporto di misura > si individua il verice V sulla semiretta parallela all’asse z e passante per il punto H’.