MACRO- COSTRUZIONE PER L’OMOLOGIA AFFINE

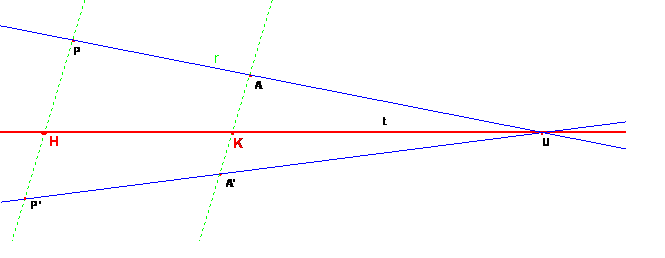
-- Disegnare la retta t, asse di omologia

-- Segnare i due punti A e A’ che si corrispondono in questa omologia

-- Segna un punto P (di cui vogliamo individuare il corrispondente nell’omologia di asse t)

-- Tracciare la retta r , passante per A e P

-- Indicare con U il punto di intersezione della retta r con la retta t

-- Disegnare la retta r’ che congiunge A’ con U

-- Disegnare la retta che congiunge A e A’

-- Disegnare la retta passante per P // ad AA’

-- Il punto di intersezione fra quest’ultima retta e r’ sarà il punto P’

Ora si può definire la macro

-- Scegliere per gli <oggetti iniziali> l’asse t, i punti A, A’, P

-- Scegliere per gli <oggetti finali> il punto P’

-- Ora si può, con <definizione macro> completare la costruzione, indicando nell’<aiuto> anche l’ordine delle operazioni, cioè <dato l’asse e due punti corrispondenti, costruisce l’omologo di un punto dato>. Ricordarsi di salvare la macro come <file> altrimenti allo spegnimento del pc verrà eliminata.

Tale corrispondenza è biunivoca, la retta t , asse di omologia, è luogo di punti uniti; a rette parallelele corrispondono rette parallele, rimane invariato il rapporto semplice di tre punti allineati, cioè

AK / A’K = PH / P’H

Tale rapporto si mantiene costante pertanto l’omologia può essere anche definita a partire dall’asse, dalla direzione r (r diverso t) e dalla costante.

Cosa succede quando la retta AP risulta parallela all’asse t ?

La costruzione sarà analoga, si sostituirà il punto U con la direzione r