Classificazione delle isometrie

Le isometrie studiate finora sono:

• Simmetrie assiali
• Rotazioni
• Traslazioni
• Antitraslazioni

Vogliamo ora classificarle e dimostrare che queste sono tutte e solo le isometrie possibili.

Possiamo suddividere tutte le isometrie del piano in due classi:

• le isometrie dirette, cioè che conservano l’orientamento dei punti
• le isometrie inverse, che invertono l’orientamento dei punti (come la simmetria assiale)

In altri termini l’ordinamento dei punti è un elemento invariante per le isometrie dirette, mentre non lo è per le isometrie inverse.

Se invece consideriamo l’esistenza o meno di punti uniti, possiamo ugualmente suddividere tutte le isometrie in altre due classi: quelle con punti uniti e quelle prive di punti uniti.

Possiamo riassumere tutto nel seguente schema riassuntivo:

Schema riassuntivo delle isometrie piane
	Isometria con punto fisso	Isometrie senza punti fissi
Isometrie dirette	Rotazioni (in particolare simmetrie centrali)	Traslazioni (di un vettore non nullo v)
Isometrie inverse	Simmetrie assiali	Antitraslazioni (di un vettore v)

Composizione di isometrie

È possibile applicare successivamente più di una isometria: qual è il risultato? si ottiene ancora una isometria. Infatti possiamo notare che componendo due trasformazioni si ottiene ancora una trasformazione.
Siano:
A e B due punti del piano
A’ il trasformato di A e B’ il trasformati di B rispetto ad una isometria f
A’’ il trasformato di A’ e B’’ il trasformato di B’ rispetto ad una isometria g
Allora:
quindi per la proprietà transitiva della congruenza

Possiamo affermare che: la composizione di più isometrie è ancora un’isometria

Esaminiamo alcuni esempi
Osservazione: in generale la composizione di più isometrie non è commutativa. L’illustrazione fornisce un esempio.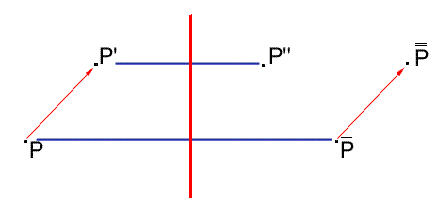

                                  

1. Composizione di due traslazioni:

Due traslazioni successive equivalgono ad una traslazione. Si può notare che tale composizione è commutativa cioè: Tc = Ta • Tb = Tb • Ta

2. Composizione di due rotazioni con lo stesso centro:

Due rotazioni successive di ugual centro equivalgono ad una rotazione. Si può notare che tale composizione è commutativa, cioè: Rc = Ra • Rb = Rb • Ra

Composizione di simmetrie assiali

Teorema 1: La composizione di due simmetrie assiali con assi incidenti equivale ad una rotazione avente centro nel punto di intersezione degli assi ed ampiezza doppia dell’angolo da essi formato.

Come conseguenza di quanto detto, anche la composizione di due simmetrie assiali con gli assi perpendicolari equivale ad una rotazione di un angolo piatto, cioè ad una simmetria centrale.

Teorema 2: La composizioni di due simmetrie assiali con gli assi paralleli e distinti equivale ad una traslazione di un vettore di direzione perpendicolare agli assi, con il verso dal primo al secondo asse, e modulo doppio della loro distanza. Se i due assi coincidono si ottiene l’identità.

Teorema 3: La composizioni di tre simmetrie assiali i cui assi sono due paralleli fra loro e l’altro ad essi ortogonale, è una antitraslazione.

Osservazione: Da quanto detto si può dedurre che una rotazione o una traslazione si possono ottenere mediante composizione di due simmetrie assiali. Mentre attraverso la composizione di tre simmetrie assiali possiamo ottenere un’antitraslazione.