Ci sono infinite isometrie; d’altra parte tutte queste si possono ricondurre a quattro tipi fondamentali:

• simmetria assiale
• rotazione (in particolare simmetria centrale)
• traslazione
• antitraslazione

Queste particolari trasformazioni sono importanti perché vedremo che ogni altra isometria può essere ottenuta come composizione di queste.

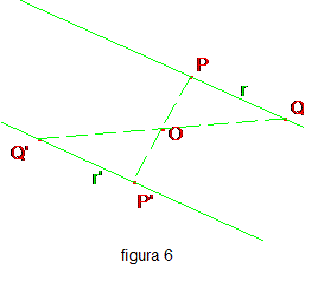
Simmetrie assiali. Fissata una retta a si dice simmetria assiale di asse a la corrispondenza che associa ad ogni punto P del piano non appartenente ad a il punto P’ situato sulla retta per P perpendicolare ad a, nel semipiano opposto, rispetto ad a, a quello contenente P e alla stessa distanza di P da S. Se P appartiene ad a allora P’ coincide con P.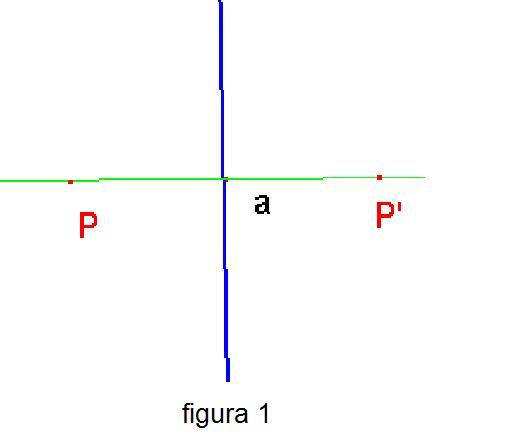

                                               

Nella simmetria assiale di asse a il punto P’ è detto “simmetrico” di P rispetto ad a e più in generale la figura F', trasformata della figura F, è detta “simmetrica” di F rispetto ad a.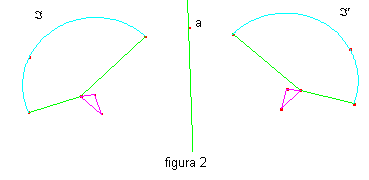

                                                              

La seconda figura mostra due figure simmetriche nella simmetria di asse a.
Si dimostra facilmente che ogni simmetria assiale è una isometria.
Una proprietà comune a tutte le isometrie è quella di trasformare rette in rette, cioè se A,B,C sono tre punti distinti allineati anche i loro corrispondenti A’,B’,C’ sono distinti e allineati.
Inoltre, per una simmetria assiale di asse a risulta:

• se il punto P’ è il simmetrico del punto P allora P è il simmetrico di P’, quindi ogni simmetria assiale è una involuzione
• la simmetrica r’ di una retta r parallela ad a è parallela anch’essa ad r e situata alla stessa distanza di r da a (fig. 3 a)

                                  

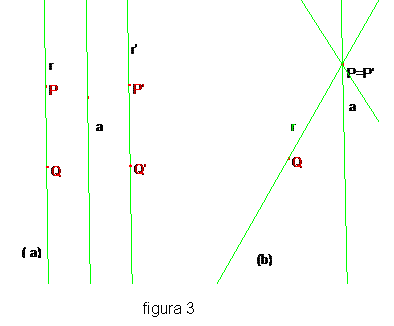
mentre la simmetrica r’ di una retta r incidente a in un punto P è nch’essa incidente r ancora in P e forma lo stesso angolo che r forma con a

• l’asse a è una retta unita, formata da punti uniti
• ogni retta perpendicolare ad a è una retta unita, il cui unico punto unito è quello di intersezione con l’asse

Osserviamo che una simmetria assiale “inverte il senso delle rotazioni” nel piano, ossia se tre punti non allineati A,B,C si susseguono in senso orario, i loro simmetrici A’,B’,C’ si susseguono in senso antiorario. Per tale motivo le simmetrie assiali si dicono “isometrie inverse”.
In una simmetria assiale, presi due punti A,B situati su una retta perpendicolare all’asse e sulla quale sia stato fissato un verso di percorrenza, se A precede B allora B’ precede A’; per questo motivo si dice che una simmetria assiale con asse “verticale” scambia la destra con la sinistra.
Notiamo infine che per individuare l’asse di una simmetria assiale data è sufficiente conoscere una coppia di punti corrispondenti P e P’ distinti oppure due punti uniti distinti Q e R; nel primo caso l’asse di simmetria è l’asse del segmento PP’, nel secondo è la retta QR stessa.

Simmetrie centrali. Fissato un punto O, si dice “simmetria centrale di centro O” la corrispondenza che associa ad ogni punto P del piano diverso da O il punto P’ situato sulla retta OP, alla stessa distanza di P da O e nella semiretta opposta rispetto ad O (fig. 4). Se P concide con O allora P’ coincide con O.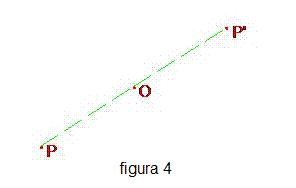

                                                         

Nella simmetria centrale di centro O il punto P’ è detto ancora “simmetrico” di P rispetto ad O e la figura F' trasformata della figura F, è detta ancora “simmetrica” di F rispetto ad O.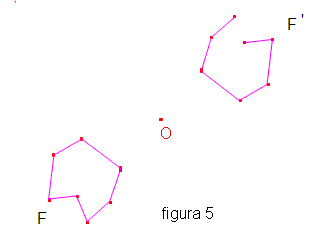

                                                     

La figura 5 mostra due figure simmetriche nella simmetria di centro O.
Come le simmetrie assiali anche le simmetrie centrali sono isometrie.

Si ha poi che la simmetria centrale di centro O:

• è una involuzione;
• trasforma ogni retta r in una retta r’ parallela ad r (fig. 6)
• trasforma ogni retta per O in se stessa, quindi le rette per O sono rette unite il cui unico punto unito è O
• trasforma ogni circonferenza di centro O in se stessa, quindi ogni circonferenza di centro O è unita
• trasforma O in se stesso, quindi O è punto unito (ed è l’unico)

                                                     

Contrariamente alle simmetrie assiali, le simmetrie centrali conservano il senso delle rotazioni nel piano, e per tale motivo le simmetrie centrali si dicono “isometrie dirette”.
Per individuare il centro di una simmetria centrale data è sufficiente conoscere una coppia di punti corrispondenti P e P’distinti, poiché in tal caso il centro di simmetria è il punto medio del segmento PP’. Se invece P coincide con P’il centro di simmetria è P stesso.

Rotazioni. Dati un angolo orientato a, cioè un angolo con verso fissato, e un punto O, si dice “rotazione di centro O e angolo orientato a” la corrispondenza che associa ad ogni punto P del piano diverso da O il punto P’situato sulla circonferenz a di centro O e raggio OP tale che PÔP’ = a.
Se P coincide con O allora P’ coincide con O.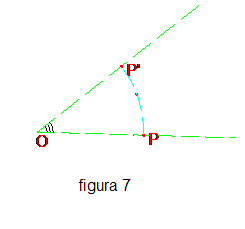

                                                     

Se l’angolo a è l’angolo nullo o l’angolo giro, si ottiene l’identità.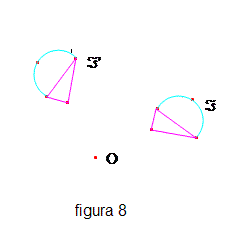

                                                     

La figura 8 mostra due figure F e F' dove F' è ottenuta da F mediante la rotazione di centro O e angolo orientato a .
Anche le rotazioni sono isometrie ed inoltre, una rotazione di centro O:

• trasforma ogni retta passante per O in una retta passante anch’essa per O
• trasforma O in se stesso, quindi O è punto unito (ed è l’unico se la rotazione non è l’identità)
• trasforma ogni circonferenza di centro O in se stessa, quindi ogni circonferenza di centro O è unita

E’facile rendersi conto che la simmetria centrale di centro O è la rotazione di centro O di un angolo piatto.
Le rotazioni non sono involuzioni (fatta eccezione per le simmetrie centrali e l’identità); sono tutte “isometrie dirette”.
Per individuare il centro e l’angolo orientato di una rotazione data è sufficiente conoscere due coppie di punti corrispondenti P, P’ e Q,Q’ : il centro O di rotazione è il punto di intersezione degli assi dei segmenti PP’ e QQ’ se essi non sono paralleli, altrimenti è il punto di intersezione delle rette PQ e P’Q’; l’ampiezza dell’angolo di rotazione è quella dell’angolo PÔP’ (o QÔQ’) e il verso è quello che porta la semiretta OP a sovrapporsi alla semiretta OP’ (o la semiretta OQ a sovrapporsi alla semiretta OQ’).

Traslazioni. Dato un segmento orientato AB, cioè un segmento con direzione e verso di percorrenza fissato (da A a B), si dice “traslazione del segmento orientato AB ” la corrispondenza che associa ad ogni punto P del piano il punto P’ tale che il segmento orientato PP' sia parallelo, di ugual lunghezza e verso concorde al segmento orientato AB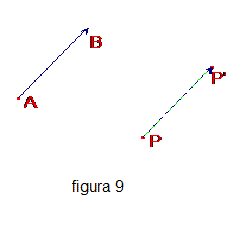

                                                     

Dalla definizione segue che ogni altro segmento orientato avente la stessa lunghezza e la stessa direzione di AB e verso concorde, individua la stessa traslazione.
Se i due estremi A e B del segmento coincidono, la corrispondenza individuata è l’identità.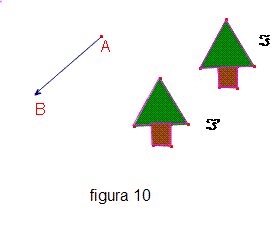

                                                     

La figura 10 mostra due figure F e F' , dove F' è ottenuta da F mediante la traslazione di segmento orientato AB.
Anche le traslazioni sono isometrie ed inoltre la traslazione di segmento orientato AB:

• trasforma ogni retta r in una retta r’ parallela ad r (fig. 11)
• trasforma ogni retta parallela ad AB in se stessa, quindi ogni retta parallela ad AB è una retta unita.

                                                     

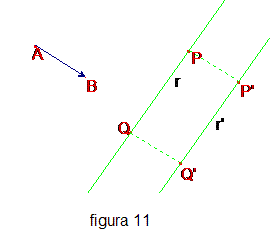
Una traslazione (che non sia l’identità) non ha punti uniti, non è una involuzione ed è una isometria diretta.
Per individuare il segmento orientato di una traslazione è sufficiente conoscere una coppia di punti corrispondenti P, P’, infatti il segmento orientato PP' individua la traslazione.

Antitraslazioni. Le “antitraslazioni” sono le isometrie ottenute componendo una traslazione (diversa dall’identità) con una simmetria assiale il cui asse sia parallelo al segmento orientato della traslazione (fig. 12).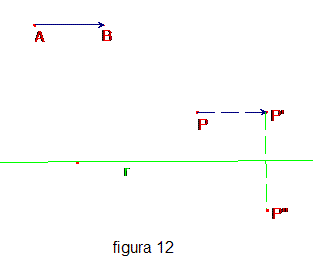

                                                     

Notiamo che il risultato di tale composizione non dipende dall’ordine con cui le due trasformazioni vengono applicate.

                                            

La figura 13 mostra due figure F e F' dove F' è ottenuta da F mediante un’antitraslazione.
Le proprietà di una antitraslazione sono ovviamente legate alle proprietà delle trasformazioni che la generano.
Un’antitraslazione è dunque un’isometria la cui unica retta unita è l’asse della simmetria assiale, non ha punti uniti, non è una involuzione ma è una isometria inversa.
Per individuare l’asse e il segmento orientato di una antitraslazione data è sufficiente conoscere due coppie di punti corrispondenti P, P’e Q,Q’:

• l’asse della simmetria è la retta che unisce i punti medi dei segmenti PP’e QQ’
• il segmento orientato della traslazione è la proiezione del segmento PP’(o QQ’) sull’asse, orientato dalla proiezione di P verso quella di P’ (orientato dalla proiezione di Q verso quella di Q’)

Osservazione: se il vettore non è parallelo all’asse si ottiene o una simmetria assiale(vettore perpendicolare all’asse) oppure una antitraslazione