| 3.1 Analyse des infiniment petits pour l'intelligence des lignes courbes: il primo manuale sul calcolo infinitesimale (1696) (a cura di Anna Chiara Zagati) |
|
Il manuale raccoglie ed organizza definizioni, corollari e proposizioni. In ogni sezione l'Hôpital pone delle domande o supposizioni a cui poi cerca di trovare una soluzione, e, inoltre, sono presenti molti esempi di calcolo pratico. La prima sezione descrive i principi del calcolo differenziale e viene infatti intitolata Dove diamo le regole del calcolo delle differenze, vi troviamo tutte le regole base del calcolo, come la regola di dervazione di un prodotto o quella di derivazione di un quoziente. Nella seconda sezione del manuale l'Hôpital determina la tangente di una curva. Data la definizione di curva come poligono con un numero infinito di lati ciascuno di lunghezza infinitamente piccola, definisce la tangente in un punto della curva come il prolungamento del lato infinitamente piccolo del poligono in quel punto; inoltre fornisce molti esempi di determinazione di tangenti. Nella terza sezione considera i problemi di massimo e minimo fornendo esempi di meccanica e geografia. Nelle sezioni successive prende in considerazione i punti di flesso, cuspidi, curvatura, curve caustiche, evolvente, e derivate di ordine superiore. Nella sezione 9, intitolata Soluzione di qualche problema che dipende dai metodi precedenti, si trova la regola, nota come regola di l'Hôpital, per trovare il limite di una funzione costituita come una frazione il cui numeratore e denominatore tendono entrambi a zero o ad infinito in un punto. Sono due le definizioni principali sul calcolo date nella prima sezione: Definizione 1: Le quantità variabili sono quelle che aumentano o diminuiscono continuamente mentre una quantità costante rimane la stessa mentre altre variano. Definizione 2: La parte infinitamente piccola con cui una quantità variabile aumenta o diminuisce continuamente viene chiamata differenziale di quella quantità . La discussione sulla regola di l'Hôpital, invece, si trova alle pagine 145-147. Essa viene presentata partendo da un problema in cui si parla di curve: Sia AMD una linea curva (AP = x; PM = y; AB = a, Fig.130) tale che il valore dell'applicazione y sia espresso con una frazione, dove il numeratore e il denominatore diventano ciascuno zero quando x = a, cioè quando il punto P cade sul punto dato B. Si domanda quale deve essere allora il valore dell'applicata BD. La figura di l'Hôpital tra l'accusa di plagio e l'amore per la matematica La figura del marchese l'Hôpital può suscitare opinioni contrastanti: si deve effettivamente a lui qualche merito matematico? E poi, quanto fu moralmente corretto il patto che siglò con Bernoulli? Abusò della sua condizione benestante e della sua posizione aristocratica per sottrarre le scoperte matematiche di altri? Non è facile uniformare un giudizio sulla sua persona. Sicuramente il marchese provò da sempre un grande amore per la matematica e da subito capì la grande importanza e l'impatto che avrebbe avuto il calcolo infinitesimale. Probabilmente fu proprio questo suo interesse verso la conoscenza del calcolo a spingerlo a stringere il tanto discusso accordo con Bernoulli. Senz'altro l'acquisizione delle scoperte e dei risultati del matematico svizzero tramite un vero e proprio pagamento può essere giudicata come un gesto illegittimo e moralmente scorretto. L'Hôpital effettivamente comprò il tempo, le lezioni e più in generale parte della produzione matematica di Bernoulli, ma forse non tanto spinto dal desiderio di emergere come grande matematico, quanto più dall'amore e dall'interesse che ebbe per la materia. E proprio grazie agli appunti e alle lezioni di Bernoulli, nonchè all'impegno, alla dedizione e alla profonda comprensione del calcolo leibniziano dello stesso marchese, fu pubblicato il primo manuale sul calcolo. Il grande contributo che l'Hôpital diede alla matematica fu quest'opera magistrale, che divenne il principale strumento di insegnamento e di diffusione del calcolo a Parigi, e poi in Europa. Al di là dei contenuti che l'Hôpital potè aver sottratto a Bernoulli, l'Analyse resterà il primo libro di testo sul calcolo, che fu pioniere della sua diffusione e divenne poi il modello per tanti manuali successivi. |
| 3.2 Il problema della brachistocrona (a cura di Gaia Bertaglia) |
| Il problema della brachistocrona (o curva di discesa
più rapida), venne formulato e pubblicato nel giugno del 1696 da Johann
Bernoulli sulla rivista tedesca Acta Eruditorum, in
un articolo intitolato Problema novum ad cujus solutionem
Mathematici invitantur. Bernoulli formulò il problema in questo modo: "Dati due punti A e B in un piano verticale, trovare il percorso AMB per il punto materiale M, discendente per la sua stessa gravità , in modo tale che esso si muova dal punto A al punto B nel minor tempo possibile." 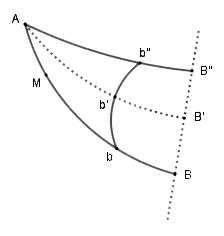 Il problema venne formulato nel pieno della disputa sulla priorità del calcolo infinitesimale, e contribuì ad inasprire il rapporto tra le parti, come sottolinea lo storico Rupert Hall, nella traduzione di D. Panzieri, del suo Philosophers at war: the quarrel between Newton and Leibniz: "In realtà sembra che intenzione di Bernoulli fosse semplicemente di separare gli uomini dai bambini, e di mostrare la superiorità dei tedeschi sugli inglesi e sui francesi, che si erano disputati a lungo la supremazia in campo matematico." (Hall 1982) Per quanto riguarda la soluzione del problema, Johann sfruttò l'analogia tra il movimento di caduta dei gravi e il movimento di propagazione della luce studiato da Fermat nel 1629, a cui si ispirò in seguito la legge di Snell sulla rifrazione della luce. La soluzione del fratello Jakob, invece, è prettamente geometrica ed è costituita da un susseguirsi di proporzioni tese a dimostrare che la curva di discesa più rapida sia proprio la cicloide. La cicloide, che risolve il problema della brachistocrona, è la curva generata da un punto fisso su una circonferenza che rotola, senza strisciare, lungo una retta. Essa presenta interessanti proprietà fisiche, infatti è brachistocrona e tautocrona. Brachistocrona, perché rappresenta il percorso percorribile nel minor tempo possibile tra due punti. Tautocrona, perché un grave posto in oscillazione lungo una cicloide la percorre sempre nello stesso tempo, qualunque sia l'ampiezza dell'oscillazione. La dimostrazione del brachistocronismo fu fornita da vari autori, in particolare quella di Jakob Bernoulli venne pubblicata sul numero di maggio degli Acta Eruditorum nel 1697, mentre Christiaan Huygens dimostrò il tautocronismo nel 1659, nella sua opera Horologium oscillatorium. |
| 3.3 Malebranche e la cerchia di matematici a Parigi (a cura di Anna Chiara Zagati) |
| Nicolas Malebranche (1638-1715) fu una figura molto
carismatica nell'ambiente socio-culturale parigino del XVII secolo.
Studiò filosofia e teologia al Collège de la Marche dal 1654 al 1656 e
si laureò in lettere. Fu anche
influenzato da Leibniz che visitò Parigi nel 1672: i due si
incontrarono molte volte, ritrovandosi a discutere di idee sia sulla
filosofia che sulla matematica. Divenne professore di matematica presso
la Congregazione dell'Oratorio dal 1674. Egli ebbe una grande influenza
sullo sviluppo della matematica e della scienza, principalmente
attraverso il gruppo di studiosi che si creò attorno a lui a Parigi,
che fu considerato per molti anni come la principale cerchia di
intellettuali in Francia. Matematici come Varignon, L'Hôpital, Guisnée,
Montmort, Carré e Reyneau entrarono tutti a far parte di questo gruppo
nell'Oratorio. Una volta giunto a Parigi nel 1691, il giovane Johann Bernoulli si rivolse a Malebranche e al suo gruppo per impartire lezioni sul nuovo calcolo infinitesimale leibniziano. L'impegno e l'attività dei matematici della cerchia per imparare e studiare profondamente le tecniche del calcolo furono molto intensi, e alla fine del XVII secolo Parigi divenne uno dei prinicpali centri di diffusione del nuovo calcolo. Nel 1699 fu nominato membro onorario dell'Accademia delle Scienze di Parigi, una delle società scientifiche più famose del mondo. Negli anni successivi, l'Accademia incluse un vasto gruppo di infinitesimalisti, come Carré, Saurin, Guisnée, Montmort, sotto la guida di l'Hôpital e Varignon, già membri dell'Accademia. |
| 3.4 L'opera di Brook Taylor (a cura di Ilaria Trombini) |
L'opera Methodus incrementorum directa et
inversa di Brook Taylor fu pubblicata nel 1715 a Londra.  L'opera ebbe una grande influenza sulla matematica, sebbene abbia attirato critiche da parte di Johann Bernoulli, che accusò Taylor infondatamente di plagio. L'opera è formata da un'introduzione e da 27 proposizioni che possono essere suddivise in sei grandi sezioni: ⢠dalla I alla VI vengono trattate le equazioni flussionali ovvero le equazioni differenziali con la notazione newtoniana; ⢠dalla VII alla XII vengono illustrate le serie; ⢠dalla XIII alla XVII vengono risolti i problemi di quadratura e curvatura; ⢠dalla XVIII alla XXIII vengono mostrati i problemi con l'arco e le vele; ⢠dalla XXIV alla XXV vengono analizzati i problemi dei centri di oscillazione e di percussione; ⢠dalla XXVI alla XXVII vengono studiati i problemi della densità dell'aria e della rifrazione della luce. Teorema di Taylor Il corollario due della proposizione VII dell'opera Methodus incrementorum directa et inversa è il noto teorema di Taylor: Consideriamo un intervallo (a, b) ⊂ R ed un punto x0 ∈ (a, b). Sia f: (a, b)→ R derivabile n volte nell'intervallo (a, b), con n ≥1, e supponiamo che la derivata n-esima) sia continua nel punto x0 . Allora, definito il polinomio di Taylor di grado n 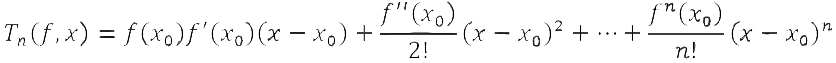 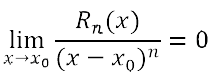 If for the evanescent increments, the fluxions of the proportionals themselves are written, now with all the v, v', v, v, v & c. equal to the time z uniformly flows to become z+v, and x becomes 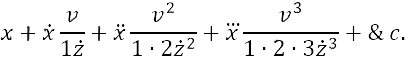 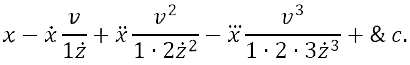 (Se per gli incrementi evanescenti, le flussioni dei proporzionali stessi sono scritte, ora con le v, v', v, v, v ecc. , uguali al tempo che z impiega uniformemente per diventare z+v, e x diventa 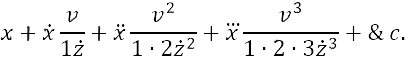 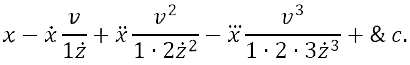 Il suddetto teorema viene insegnato oggi nei corsi di analisi matematica. Fornisce semplici formule per approssimare funzioni trascendenti come la funzione esponenziale e le funzioni trigonometriche. à il punto di partenza dello studio delle funzioni analitiche ed è fondamentale in varie aree della matematica. Il teorema permette di approssimare una funzione differenziabile nell'intorno di un punto mediante i polinomi di Taylor, i cui coefficienti dipendono solo dalle derivate della funzione nel punto considerato. I polinomi sono tra le funzioni più semplici da utilizzare. La Proposizione 17 e la discussione con Johann Bernoulli Un'altra proposizione importante presente nell'opera è la XVII.  |
| 3.5 Il calcolo infinitesimale in Italia all'inizio del XVIII secolo (a cura di Giulia Carpani) |
| Nella storia del pensiero matematico, il XVIII secolo
è caratterizzato, in modo particolare, dallo sviluppo di ricerche
connesse al moderno calcolo infinitesimale e alle sue applicazioni alla
fisica. Notevoli progressi si hanno anche in molti altri settori,
specie nell'algebra, nella geometria analitica e nella trigonometria,
grazie alla loro stretta connessione con il nuovo calcolo. Il moderno
calcolo infinitesimale nasce nel Seicento, quando Newton e Leibniz,
indipendentemente l'uno dall'altro, ne stabiliscono i metodi
fondamentali. Ma è nel corso del Settecento che i procedimenti del nuovo calcolo vengono perfezionati e arricchiti. I matematici ne estendono enormemente il campo d'applicazione, aprendo così la strada all'analisi moderna: ad esempio al calcolo delle variazioni e alla teoria delle equazioni differenziali. In Inghilterra si era diffuso il calcolo differenziale nella forma datagli da Newton, mentre nell'Europa continentale si era invece affermata la versione leibniziana del calcolo. Nell'ambiente scientifico italiano, legato a una tradizione geometrica che ha come maggiori esponenti i fratelli Ceva e Vincenzo Viviani, il calcolo leibniziano però inizia a farsi strada solo agli inizi del Settecento. La prima diffusione dell'analisi infinitesimale in Italia si deve alle numerosissime opere di Guido Grandi (1671-1742), corrispondente di Leibniz, nonché a Gabriele Manfredi, autore del primo lavoro sul calcolo infinitesimale mai pubblicato in Italia, il De constructione aequationum differentialium primi gradus (Bologna, 1707). A questa diffusione contribuiscono largamente anche Jacopo Riccati (1676-1754), noto per i suoi studi sulle equazioni differenziali, e Maria Gaetana Agnesi (1718-1799), autrice delle Istituzioni analitiche, pubblicato nel 1748. Guido Grandi e il calcolo infinitesimale Il matematico italiano che per primo pubblicò opere nelle quali vengono usati il calcolo differenziale ed integrale fu Guido Grandi. Dal 1700 Grandi iniziò lo studio dell'analisi su fonti francesi e tedesche. La prima opera pubblicata del Grandi, la Geometrica demonstratio Vivianeorum problematum (1699), riguarda il problema proposto dal Viviani sugli Acta Eruditorum del 1692, del quale Leibniz, Giacomo Bernoulli e il Viviani stesso avevano dato delle soluzioni: "Trovare una mezza sfera, ed assegnar sulla superficie curva di essa non quadrabile una porzione che sia uguale al quadrato della data retta AB". Leibniz e Bernoulli avevano risolto il problema con l'ausilio dei metodi infinitesimali, Grandi riprende la soluzione del Viviani data con i metodi classici e cerca di migliorarla integrandola con dimostrazioni basate sui metodi degli indivisibili di Cavalieri e Torricelli. Segue la discussione di altri sette problemi, dello stesso tipo del primo, dove si chiede di trovare porzioni di solidi o delle superfici non quadrabili in modo che i nuovi oggetti ottenuti siano quadrabili. Un maggiore ricorso ad algoritmi infiniti si trova nella seconda opera di Grandi: la Geometrica demonstratio theorematum Hugenianorum dedicata alla dimostrazione e al commento dei risultati che Huygens in appendice al Traité de la lumière del 1690 aveva dato, relativamente alla curva logaritmica. In questo libro sono riportati i risultati di Huygens: si tratta di quindici teoremi riguardanti proprietà della curva logaritmica, dei quali Grandi ne dà la dimostrazione in modo notevolmente prolisso.  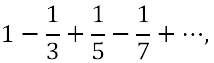 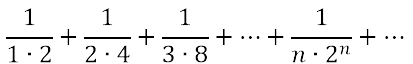 Ma ho anche inserito di quando in quando anche i dx, dy caratteristici del calcolo differenziale e il loro modo di essere differenziati e sommati. E così, se anche li avessi potuti introdurre anche nei miei opuscoli precedenti! Ma allora i segreti di quel metodo mi erano inaccessibili, mentre ora, provata la loro utilità e fecondità , perché non inserirli tra gli altri metodi a me familiari? Inoltre il significato dei simboli è molto chiaro, poiché non significa altro se non una differenza infinitamente piccola tra le stesse x e y, e facilmente troverai esposte le regole stesse del calcolo se osserverai e sfoglierai attentamente questo trattato, nel caso in cui tu non volessi ricorrere al chiarissimo L'Hospital che le spiega in modo più completo nel trattato degli infinitamente piccoli. L'utilizzo dei metodi differenziali resta in effetti piuttosto sporadico. Un'occasione per esporne alcuni rudimenti è costituita da una lettera ricevuta da Gabriele Manfredi sulla quadratura dell'iperbole che viene inserita nella seconda parte dell'opera. Per chiarire il procedimento esposto da Manfredi, Grandi infatti aggiunge una serie di note in cui spiega i passaggi e descrive le regole del nuovo calcolo nello scolio alla prop. V al Trattato:  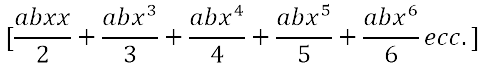 Nonostante gli evidenti limiti riscontrabili nelle sue opere, Guido Grandi è il personaggio chiave per lo studio della diffusione dei metodi del calcolo differenziale e integrale in Italia nei primi anni del XVIII secolo. Gabriele Manfredi e la matematica all'Università di Bologna Verso la fine del '600 si formò a Bologna un sodalizio di giovani studiosi interessati alle nuove scoperte nel campo della matematica e dell'astronomia; ne fecero parte i fratelli Eustachio e Gabriele Manfredi, Vittorio Francesco Stancari, Giuseppe Verzaglia. Nonostante il periodo di grave crisi che l'Università di Bologna stava attraversando, questo gruppo di giovani studiosi riuscirono a impadronirsi dei metodi della geometria cartesiana e ad affrontare con successo le tecniche del calcolo infinitesimale, lavorando modernamente ai problemi esposti nelle riviste scientifiche. Così gli scritti matematici di Gabriele Manfredi hanno una freschezza e una modernità che invano si cercherebbe in tutta l'opera di Grandi. Nel 1707 arrivò a pubblicare il De constructione aequationum differentialium primi gradus, opera che gli procurò notevole fama in Europa.  Il De Constructione ottenne l'apprezzamento generale dell'ambiente scientifico: gli Acta Eruditorum del 1708 e il Giornale de' letterati d'Italia lo recensirono molto favorevolmente; Leibniz e Giovanni Bernoulli lo lodarono. Jacopo Riccati e la matematica all'Università di Padova Diversamente dall'Università di Bologna, l'Università di Padova agli inizi del '700 godette di un periodo di notevole efficienza. La Repubblica veneta con una politica accorta di buoni stipendi, di agevolazioni e anche di tolleranza religiosa, riusciva ad assicurarsi come docenti alcuni dei migliori scienziati italiani e stranieri. Nell'ambiente veneziano e padovano del primo settecento avviene la maturazione scientifica di Jacopo Riccati. La sua formazione matematica più moderna cominciò con la lettura dei Principia di Newton, a cui si dedicò aiutato da Stefano degli Angeli; ben presto familiarizzò con i metodi della geometria cartesiana come attestano due suoi lavori databili intorno al 1705, inseriti nella raccolta delle sue opere: De solutione aequationum analiticarum et problematum geometricarum per curvas simplicissimas; De modo construendi non ineleganter Problemata plus quam solida. Nel 1710 Riccati era già introdotto nello studio del calcolo differenziale ed integrale, e ne diede un notevole contributo, soprattutto nella prima fase del suo sviluppo. Nel 1714 sul Giornale de' letterati d'Italia fu pubblicata una sua memoria contenente critiche alle osservazioni di Giovanni Bernoulli sul lavoro di Hermann sul problema inverso delle forze centrali. Giovanni Bernoulli aveva rilevato che la soluzione di Hermann non era la più generale perché nell'integrazione dell'equazione del moto 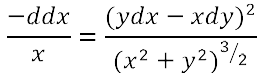 Riccati replicò con un articolo in cui è messo in evidenza il suo metodo di separazione parziale delle variabili per integrare certe equazioni differenziali. Riccati fornisce vari esempi; si riporta il primo per dare un'idea del metodo. Sia 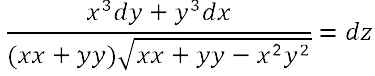 Riccati raggruppa i differenziali in modo che una parte di essi sia un differenziale esatto 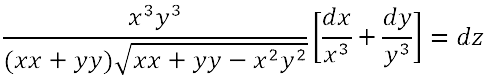 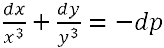 risulta risulta 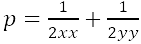 e sostituendo si perviene
all'equazione a variabili separate. e sostituendo si perviene
all'equazione a variabili separate.
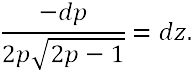 Gran parte dei risultati più significativi ottenuti da Riccati furono raccolti in un trattato composto attorno al 1723; successivamente rielaborato e inserito nelle Opere del Riccati (pubblicate postume nel 1761-1765) con il titolo: Della separazione delle indeterminate nelle equazioni differenziali del primo grado, e della riduzione delle equazioni differenziali del secondo grado e d'altri gradi ulteriori. Il trattato è diviso in tre parti e reca due appendici.  Maria Gaetana Agnesi, la prima donna matematica dell'età moderna Verso la metà del Settecento apparvero in Italia alcuni libri di introduzione al calcolo infinitesimale, più elementari del De Constructione di Gabriele Manfredi che presupponeva la conoscenza dei fondamenti dell'analisi. Tra questi, spicca il trattato in due volumi scritto dalla prima donna matematica dell'età moderna: le Instituzioni analitiche ad uso della gioventù italiana di Maria Gaetana Agnesi, pubblicato nel 1748. Si tratta di un'opera volutamente elementare, in quanto nelle intenzioni dell'autrice era indirizzata alla preparazione dei giovani studenti.  Non avvi alcuno il quale informato essendo delle Matematiche cose non sappia altresì quanto, in oggi spezialmente, sia necessario lo studio dell'analisi e quali progressi si sieno con questa fatti, si facciano tuttora, e possano sperarsi nell'avvenire; che però non voglio né debbo trattenermi qui in lodando questa scienza, che punto non ne abbisogna, e molto meno da me. Ma quanto è chiara la necessità di lei, onde la Gioventù ardentemente s'invogli di farne acquisto, grandi altrettanto sono le difficoltà che vi s'incontrano, sendo noto e fuor di dubbio che non ogni città , almeno nella nostra Italia, ha persone che sappiano o vogliano insegnarla e non tutti hanno il modo di andar fuori della Patria a cercarne i maestri. Con l'intenzione dunque di raccogliere e riordinare con chiarezza e semplicità , omettendo tutto il superfluo, sono redatti i due tomi. Il primo s'intitola Dell'analisi delle quantità finite, e si apre con l'esposizione degli elementi di algebra; si passa quindi alla teoria delle equazioni algebriche e alla geometria analitica piana per chiudere con i metodi di ricerca dei massimi e minimi. Il secondo è diviso nei tre libri Del calcolo differenziale, Del calcolo integrale, Del metodo inverso delle tangenti. Esso è dedicato al calcolo differenziale e integrale, agli sviluppi in serie, alle equazioni differenziali del primo e del secondo ordine. L'Agnesi studia molte curve piane, affette anche da singolarità complicate, argomento che sarà ripreso, con molta maggiore originalità e organicità, da Gabriel Cramer. In particolare, andarono sotto il nome di "curva" o "versiera" di Agnesi curve diverse, sebbene analoghe alla cubica piana razionale di equazione L'Agnesi scriveva:  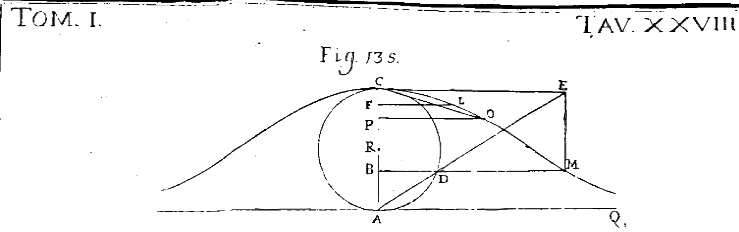 Sia M uno di questi punti, e chiamata AC=a, AB=x, BM=y, sarà per la proprietà del circolo, 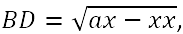 e per la condizione del problema,
sarà AB:BD=AC:BM, cioè e per la condizione del problema,
sarà AB:BD=AC:BM, cioè 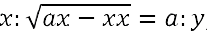 , però , però 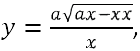 ,
o sia ,
o sia 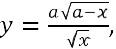 , equazione della curva da descriversi, che
dicesi la Versiera. , equazione della curva da descriversi, che
dicesi la Versiera. Eliminate le radici, l'equazione della versiera è dunque x y 2 = a 2 (a - x). Nei paesi anglosassoni la versiera è nota con il nome di witch of Agnesi (strega di Agnesi). Il motivo di questo nome non è completamente chiaro; con ogni probabilità il traduttore, non avendo molta dimestichezza con l'italiano, prese il termine versiera come sinonimo di "avversaria". In realtà , il termine versiera deriva quasi certamente dal fatto che il segmento AB che entra nella definizione della curva è il seno verso dell'angolo α in figura (il seno verso è una funzione trigonometrica oggi caduta in disuso, che è uguale a 1-cosα).  Il Giornale de' letterati d'Italia Nel 1710 iniziò la pubblicazione a Venezia del Giornale de' letterati d'Italia presso l'editore libraio Gabriello Hertz. Scopo del giornale era dare notizia dell'attività letteraria e scientifica italiana, in particolare attraverso recensioni di libri, e ospitare brevi note di carattere scientifico o erudito.  Fu dato ampio spazio alle polemiche scientifiche più vivaci sorte nell'ambito dello sviluppo dei metodi del calcolo differenziale ed integrale: quella tra Grandi e Varignon sugli spazi più che infiniti, quella tra Verzaglia e Hermann sul problema inverso delle forze centrali, quella tra Jacopo Riccati e Nicola Bernoulli. Sul Giornale de' Letterati di Venezia furono pubblicate le importanti memorie di Giulio Carlo de' Fagnano relative alla lemniscata. Dal 1710 al 1740, anni della sua pubblicazione, il Giornale di Venezia, si rivelò uno strumento indispensabile per la cultura italiana. Il calcolo infinitesimale in Italia pose profonde radici negli anni tra il 1700 e il 1710. à in questo periodo che questo metodo venne attentamente studiato non solo da Guido Grandi, Gabriele Manfredi, Verzaglia, Stancari, che sono i primi a farsi conoscere, ma anche da Jacopo Riccati, Fagnano, Maria Gaetana Agnesi ecc. ... I contributi italiani sono difficilmente rintracciabili: mancando prima del 1710 (anno in cui inizia il Giornale de' letterati) una rivista scientifica ed essendo anche l'attività editoriale in genere meno vivace che in altri paesi, molte delle riflessioni sul calcolo sono da ricercarsi nei carteggi e nelle note manoscritte. Sede primaria per lo studio del calcolo infinitesimale furono le Università : Pisa, Bologna, Padova, Roma e Napoli. Un'altra sede importante per la diffusione della cultura scientifica furono le Accademie che sorgevano quasi in ogni città importante; in molte di queste la matematica era oggetto di discussione e di studio e molti matematici ebbero posizioni di rilievo nelle accademie. L'astronomia e l'idrodinamica furono i campi nei quali in modo più diretto gli strumenti del calcolo infinitesimale trovavano le loro applicazioni e quasi tutti gli scienziati dei quali ci siamo occupati furono matematici, astronomi, idraulici. Alle competenze scientifiche dei matematici si faceva largamente ricorso come educatori, organizzatori culturali e soprattutto come consulenti in relazione ai problemi della sistemazione idraulica del territorio dell'Italia centrale. |
| 3.6 La Théorie des fonctions analytiques di Lagrange (a cura di Matteo Modonesi) |
Pubblicata a Parigi nel 1797, fu una delle opere più
studiate da intere generazioni di allievi; dimostra la preferenza di
Lagrange per una base algebrica per il calcolo, eliminando qualsiasi
tipo di visione infinitesimale.
 Per fare ciò, Lagrange interpretò lalgoritmo diretto (ovvero lalgoritmo della differenziazione) come una regola per trasformare le funzioni tale che, se applicata reiteratamente a una funzione 𝑦=𝑓(𝑥), forniva, a parte i fattori numerici, i coefficienti dello sviluppo di 𝑓(𝑥+ℎ) in serie di potenze di ℎ. Tali coefficienti vennero chiamati da Lagrange funzioni derivate e indicati con 𝑓(k)(𝑥) con 𝑘 = 1,2,3, Per ottenere il suo obiettivo Lagrange avrebbe dovuto mostrare che le funzioni derivate sostituivano i quozienti differenziali di Leibniz Pur conscio che esistevano delle eccezioni, giudicate tuttavia non rilevanti, secondo Lagrange ogni funzione 𝑓(𝑥) poteva essere espressa nella forma: Per ottenere i coefficienti 𝑝,𝑞,𝑟, procede nel seguente modo: pone Per questo sostituisce in 𝑓(𝑥 + ℎ) dapprima ℎ + 𝑜 al posto di ℎ, poi 𝑥 + 𝑜 al posto di 𝑥 (con 𝑜 indeterminata indipendente da ℎ). Naturalmente si deve ottenere lo stesso risultato. Con la prima sostituzione si ottiene 2𝑞 = 𝑝′ 3𝑟 = 𝑞′ 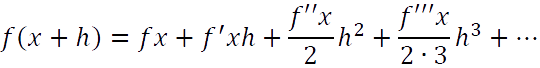 La teoria di Lagrange rappresenta il tentativo di ridurre qualsiasi funzione reale alla forma polinomiale, in modo da limitare l'uso non solo di funzioni trascendenti ma anche di funzioni irrazionali e frazionarie. In altre parole, la teoria di Lagrange viene definita algebrica in quanto riconduce lanalisi (sia finita che infinitesimale) allalgebra che risulta così alla base di tutta la matematica. Lagrange ebbe difficoltà ad imporre la sua teoria e il fallimento del suo progetto segnò, almeno sul continente, la fine del programma di analisi settecentesca iniziato da Eulero. |
| 3.7 Maclaurin e Lagrange: due approcci al calcolo fra geometria e algebra (a cura di Paolo De Fazio) |
| Il calcolo differenziale di Maclaurin
Colin Maclaurin sviluppa il calcolo differenziale nel suo Treatise of fluxions del 1742. Egli appartiene alla scuola matematica inglese e pertanto segue il modello newtoniano; l'unica sostanziale differenza è l'esclusione del concetto di infinitesimo che era stato saltuariamente usato da Newton stesso come nel caso della dimostrazione del lemma 2 del secondo libro dei Principia. La trattazione di Maclaurin è puramente geometrica e intuitiva e fa uso nella sua opera di 350 disegni che permettono una trattazione descrittiva degli oggetti matematici. Egli come il suo maestro concepisce la derivata, che analogamente indica col termine di flussione, come una velocità . Maclaurin stesso scrive, La velocità secondo cui una quantità scorre ...è chiamata flussione che è pertanto misurata dall'incremento [positivo o negativo] che sarebbe generato in un dato tempo da questo moto, se fosse uniformemente continuato da quello stesso istante senza accelerazione o decelerazione. 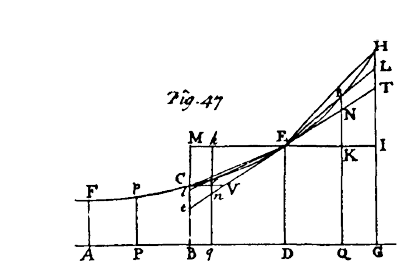 Era noto che nei punti di massimo di una curva regolare la tangente fosse orizzontale. In tempi antichi i Greci non trattarono solo le tangenti ma diedero anche le nozioni di convessità e concavità di una curva; i matematici del '700 vollero studiare più curve includendo anche quelle con punti di flesso. Maclaurin definisce a questo punto i punti di massimo in modo puramente descrittivo e senza usare disuguaglianze. Scrive infatti Quando ad un certo istante la quantità variabile all'inizio cresce fino ad un momento assegnato e poi decresce ... la sua grandezza è considerata un massimo ... In problemi di questo tipo ...la quantità variabile è rappresentata come l'ordinata della curva ... L'ordinata di un punto della curva è un massimo ... quando è più grande ... delle ordinate che possono essere disegnate dalle parti di entrambi i rami della curva adiacenti a quel punto ... . 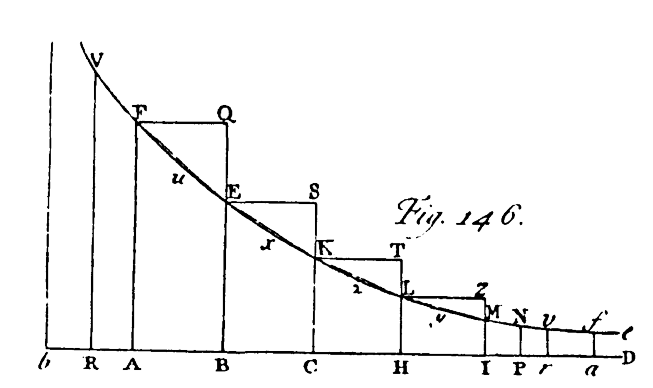 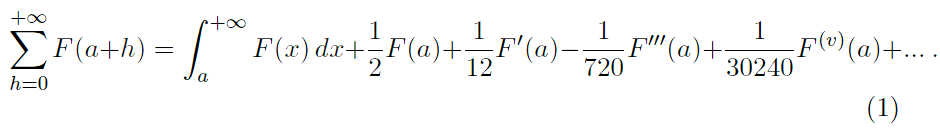 In maniera analoga, egli pertanto dimostra che 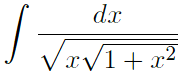 determina la lunghezza di un arco di ellisse. Questo lavoro influenzò i
lavori di d'Alembert, Eulero e Legendre nella ricerca di una forma
canonica per integrali
ellittici.
determina la lunghezza di un arco di ellisse. Questo lavoro influenzò i
lavori di d'Alembert, Eulero e Legendre nella ricerca di una forma
canonica per integrali
ellittici. Il calcolo differenziale di Lagrange Il calcolo differenziale di Lagrange, sviluppato nel trattato Théorie des fonctions analytiques del 1797, rappresenta un punto di svolta nello sviluppo dello stesso in Europa. Egli conosceva sia il lavoro di Newton sia quello di Leibniz ma nel suo lavoro seguirà l'impostazione di quest'ultimo. Tuttavia si discosta anche dalla teoria leibniziana poiché il calcolo, secondo lo stesso Lagrange non deve essere soggetto né ad alcuna intuizione di moto o velocità né tantomeno ad un concetto intuitivo di infinitesimo o limite. Tutto ciò viene definito tramite processi da lui considerati puramente algebrici e agli argomenti dei suoi predecessori sostituisce l'analisi algebrica di quantità finite. Egli basa la sua nuova teoria sull'assunto che lo sviluppo di una funzione in serie di potenze sia un'operazione prettamente algebrica come gli appare quando ottiene 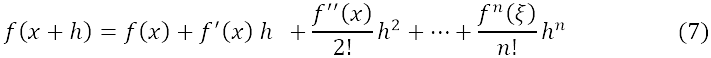 E' singolare vedere come gli approcci di Maclaurin e Lagrange siano diversi ma funzionali alla formalizzazione di risultati molto simili. Singolare è anche osservare come concepiscono gli oggetti fondamentali del calcolo: le funzioni. Il termine funzione comparirà per la prima volta nel lavoro del 1684 Nova Methodus pro Maximis et Minimis, itemque Tangentibus di Leibniz e Lagrange nella Théorie des fonctions analytique scrive: Si chiama funzione di una o più quantità , ogni espressione del calcolo nella quale queste quantità entrano in maniera qualunque, insieme o no con altre quantità che si considerano aventi dei valori dati e costanti, mentre le quantità delle funzioni possono assumere ogni valore possibile. Maclaurin invece segue l'impostazione dello stesso Newton il quale, nel suo saggio Come tracciare tangenti a linee meccaniche ragiona in termini di moto. Nella descrizione di qualsivoglia linea meccanica si possono trovare due momenti del genere che combinano o compongono i movimenti del punto che la descrive, e grazie a quei due movimenti si può trovare il movimento [risultante] di quel punto, la cui determinazione è in una tangente alla linea curva. Pertanto è evidente che la definizione di Lagrange si avvicini a quella odierna. La definizione di Newton invece fa riferimento ai concetti di linea meccanica e di curva poiché suo interesse è rivolto a studi cinematici. In un linguaggio moderno potremmo vedere le equazioni parametriche della traiettoria di un punto materiale che si muove nel piano (x(t); y(t)), dove t ∈ I ⊆ R, le flussioni delle variabili x e y (fluenti nel linguaggio newtoniano) coincidono con i differenziali rispetto al tempo delle funzioni x e y e vengono rispettivamente notate con La critica fu piuttosto dura con lapproccio inglese. Fra i maggiori oppositori troviamo George Berkeley che nel 1734 scrive The Analyst sotto forma di lettera a un matematico infedele comunemente ritenuto essere Edmond Halley. Berkeley critica Newton proponendo in primis tesi di matrice greca. Infatti trova difficile pensare sia le "velocità astratte di tali imperfette quantità nascenti" sia quantità infinitamente piccole. La critica di Berkeley sottolineava loscurità degli oggetti così definiti e scrive: cosa sono queste flussioni? Le velocità di incrementi evanescenti. E cosa sono questi incrementi evanescenti? Essi non sono quantità finite, non sono infinitesimi, non sono niente. Ed allora dobbiamo chiamarli spettri di quantità morte? Il Treatise of fluxions di Maclaurin nasce anche a seguito del lavoro di Berkeley e si offre di dare solidità alla teoria di Newton. Maclaurin altresì riconosce il fondamento delle tesi di Berkeley e rivendica l'uso nel suo trattato del rigore dei geometrici greci. Evita inoltre l'uso del concetto di infinitesimo usando nella sua trattazione solo i concetti di moto e velocità assunti come evidenti. Nella prefazione scrive: L'autore di quel lavoro [Berkeley] aveva presentato il metodo delle flussioni come fondato su un falso ragionamento e pieno di misteri. Le sue motivazioni sembrano essere state motivate in gran parte dalla maniera concisa in cui gli elementi di questo metodo sono stati di solito descritti; e l'essere stato frainteso da una persona delle sue capacità mi è sembrata una prova sufficiente che si richiedesse una trattazione più completa dei loro fondamenti. Maclaurin tuttavia non riuscirà nel suo intento e non convincerà i matematici del continente. Riportiamo le considerazioni di Lagrange che, poiché segue una trattazione algebrica del calcolo, non approva l'introduzione di una idea ad esso estranea: la velocità . Pertanto nella Théorie des fonctions analytique scrive: Ma, da un lato, introdurre il movimento in un calcolo che non ha che quantità algebriche per oggetto è introdurre una idea estranea, che costringe a considerare queste quantità come linee percorse da un mobile; d'altro lato bisogna riconosce che non si abbia affatto una idea ben chiara di cosa sia la velocità istantanea di un punto, quando questa velocità è variabile; e si può vedere nel dotto "Trattato delle flussioni" di Maclaurin come sia difficile dimostrare rigorosamente il metodo delle flussioni, e quanti artifici particolari occorra impiegare per dimostrare le diverse parti di questo metodo. Osserviamo infine come anche l'impostazione algebrica dello stesso Lagrange verrà anch'essa criticata. Infatti nel suo Cours d'analyse (1821) Cauchy si interroga sulla questione dei metodi dell'analisi ed afferma che abbia cercato di ricorrere a tutto il rigore che si esige in geometria con la finalità di non ricorrere mai ai "ragionamenti tratti dalla generalità dell'algebra". Egli continua asserendo che: ... [i ragionamenti tratti dalla generalità dell'algebra] non possono essere considerati, mi sembra, che come delle intuizioni adatte a far talvolta presentire la verità , ma che poco si accordino con l'esattezza tanto vantata delle scienze matematiche. |