Cap. III

L'aritmetica dall'India all'Europa

Uno sguardo particolare va rivolto ai sistemi di numerazione indiano e arabo, dai quali ha avuto origine il sistema posizionale decimale diffuso in Europa.

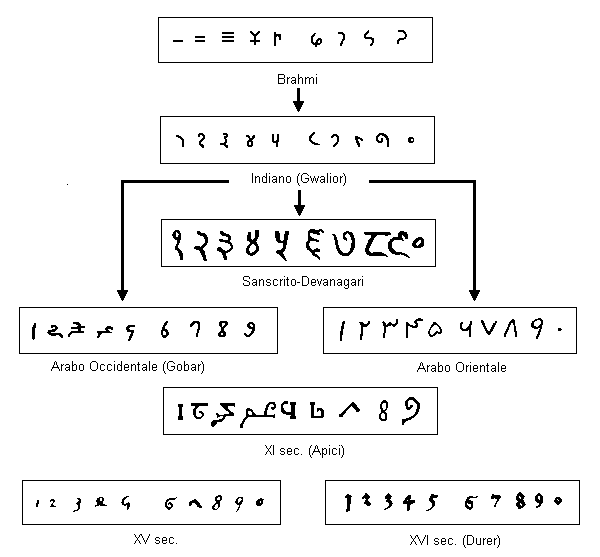
Dopo aver analizzato i diversi sistemi di numerazione e come si sono evoluti nel tempo, viene riportato qui di seguito l'albero genealogico delle nostre cifre, secondo Karl Menninger.

L'introduzione del sistema di numerazione indo-arabico in Europa, con il sistema posizionale e il simbolo per lo zero, rese considerevolmente più semplici i calcoli aritmetici. Non si sa esattamente quando questo nuovo sistema sia entrato in Europa: il manoscritto più antico contenente numeri arabi è il Codex Vigilanus, scritto in Spagna nel 976. La sua diffusione, però, è legata essenzialmente a due nomi: da una parte l'opera di al-Khuwarizmi tradotta in latino e diffusa attraverso la Spagna con il sistema delle Università; dall'altra l'opera di Leonardo Pisano e il contributo delle scuole d'abaco.

Nella seconda metà dell'VIII secolo, Baghdad divenne un fiorente centro culturale: grazie al mecenatismo di tre grandi protettori della cultura (al-Mansur, Harun ar-Rashid e al-Mamun) la città diventò una nuova Alessandria. Come il Museo ad Alessandria, così a Baghdad fu fondata una "Casa del Sapere", che accolse scienziati e filosofi provenienti dal Medioriente e dal mondo cristiano. Fra i suoi membri vi era il matematico e astronomo Mohammed ibn-Musa al-Khuwarizmi. Questo scienziato, tra le altre cose, scrisse due opere di aritmetica e algebra: di una di queste ci è pervenuta soltanto una traduzione latina recante il titolo De numero indorum (Sul calcolo numerico indiano). In quest'opera, al-Khuwarizmi presentava una esposizione così completa del sistema di numerazione indiano (da come cambia il valore del numero cambiando di posto, all'importanza dello zero, alle operazioni basate su questo sistema) che fu forse per questo che si diffuse l'errata convinzione che il nostro sistema di numerazione fosse di origine araba. La nuova notazione diventò familiare con il nome di al-Khuwarizmi o algorismi; infine lo schema di numerazione facente uso di cifre indiane venne chiamato algorismo o algoritmo, termine usato oggi con altro significato.

Attraverso le traduzioni in latino, molte opere arabe ebbero la possibilità di diffondersi in tutta Europa: tra queste c'era anche l'opera di al-Khuwarizmi. Leonardo Pisano studiò una di queste traduzioni. Esso, noto anche come Fibonacci (come abbreviazione di filius Bonacci), era figlio di un funzionario dello Stato e, per seguire il padre nei suoi impegni, aveva viaggiato in Egitto, Siria, Grecia e Algeria: era pertanto naturale che Fibonacci si impregnasse di metodi algebrici arabi, compreso il sistema di notazione indo-arabico. Per avere altre notizie sul matematico è possibile accedere al sito Chi era Fibonacci? [53]. La sua opera più importante, Liber abaci, completata nel 1202, discute in maniera esauriente metodi e problemi algebrici, difendendo decisamente l'uso delle cifre indo-arabiche. Nel libro (in latino) descrive "le nove figure indiane" insieme al segno 0 e le regole che tutti noi impariamo alle scuole elementari per sommare, sottrarre, moltiplicare e dividere.

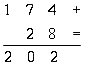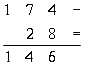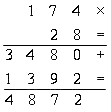Dopo aver spiegato i procedimenti aritmetici, compresa l'estrazione di radici, si addentra in problemi relativi a transazioni commerciali, usando un complicato sistema di frazioni nel calcolo di cambi di monete.
Purtroppo, il principale vantaggio della notazione posizionale, la sua applicabilità alle frazioni, è sfuggito quasi totalmente a coloro che usarono le cifre indo-arabiche durante il primo millennio della loro esistenza. Anche Fibonacci, nella sua opera, usa le frazioni a numeratore unitario e le frazioni comuni e presenta tavole di conversione per passare dalle une alle altre. La frazione , per esempio, viene trasformata in e in .
L'utilizzo di una strana notazione lo portava ad esprimere la somma di e nella forma , che stava ad indicare .

Tra i problemi trattati nel Liber abaci, sicuramente il più famoso è il seguente:

Quante coppie di conigli verranno prodotte in un anno, a partire da un'unica coppia, se ogni mese ciascuna coppia dà alla luce una nuova coppia che diventa produttiva a partire dal secondo mese?

Questo problema dà origine alla Serie di Fibonacci [54]: 1, 1, 2, 3, 5, 8, 13, 21, .., , .. dove .

L'Europa occidentale si dimostrò molto aperta verso la matematica araba, più di quanto non lo fosse stata con la geometria greca. L'abbandono del vecchio sistema numerico romano, però, avvenne molto lentamente. Ciò forse perché era abbastanza diffuso il calcolo con l'abaco che era abbastanza semplice col vecchio sistema, ma che non era possibile con il nuovo. I numeri non potevano essere raggruppati in verticale per fare le addizioni, le sottrazioni, le moltiplicazioni e le divisioni e perciò i vantaggi del nuovo sistema non erano così evidenti come nel calcolo con carta e penna. Inoltre, il segno 0 non esisteva, rendendo impossibile mostrare l'assenza del numero in una determinata colonna.
Malgrado la popolarità del libro di Fibonacci tra gli scolari, il primo manoscritto francese ad usare il nuovo sistema di numerazione fu scritto nel 1275. Il sistema di numerazione greco rimase popolare nelle regioni attorno all'Adriatico ancora per molti anni. Per molti secoli vi fu una forte competizione tra "abacisti" e "algoristi" [55] e questi ultimi trionfarono definitivamente solo nel XVI secolo.