un cilindro munito della topologia indotta da R³. Definiamo poi M come l'insieme delle coppie di punti di C del tipo {p,-p}, ossia:

dove ovviamente è p=(x,y,z) e -p=(-x,-y,-z). L'esistenza di una suriezione naturale da C in M ci permette di dotare M della topologia quoziente, lo spazio che ne risulta è detto appunto Nastro di Möbius.
Consideriamo la funzione

Inoltre M risulta omeomorfo a f(M), sottoinsieme di R³, con la topologia indotta; infatti la proprietà universale del quoziente e la continuità dell'applicazione

Anche il cilindro può essere rappresentato come spazio quoziente. Considero il quadrato unitario X={ (x,y) in R² | 0<= x,y<= 1} con la topologia indotta da R³ e definiamo una relazione di equivalenza, ~,su X in questo modo: (x,y)~(x',y') <==> (x,y)=(x',y') oppure {x,x'}={0,1} e y=y'. Lo spazio quoziente che ne risulta, X/~, è omeomorfo al cilindro. Intuitivamente possiamo vederlo in questo modo:

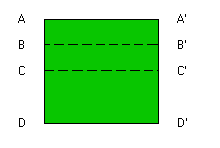
Il Nastro di Möbius può essere ottenuto in modo analogo: ancora una volta partiremo dal quadrato unitario ma questa volta la relazione di equivalenza sarà la seguente: (x,y)~(x',y') <==> (x,y)=(x',y') oppure {x,x'}={0,1} e y=1-y'.
Vediamo come, da questa relazione di equivalenza sul quadrato, otteniamo il Nastro di Möobius:

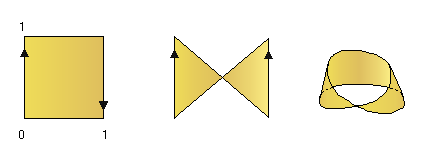
Mentre per il Cilindro i punti identificati erano simmetrici rispetto un asse che tagliasse verticalmente il quadrato unitario, nel caso del Nastro di Möbius sono simmetrici rispetto il punto di incontro delle diagonali del quadrato:

Torneremo in seguito a confrontare altri aspetti del Cilindro e del Nastro, per il momento vogliamo vedere che relazione intercorre tra il piano proiettivo, P² e il Nastro di Möbius.

Il piano proiettivo reale, P²=P(R³), è definito come S²/~, dove S² è la sfera unitaria e ~ è una relazione di equivalenza così definita: x ~ x' <==> x = +x' o x = -x'. In questo modo l'emisfero settentrionale della sfera è identificato con quello meridionale, possiamo quindi concentrare la nostra attenzione su uno di essi. L'emisfero è omeomorfo al disco chiuso D²={ (x,y) in R² | x²+y²<=1 } tramite l'omeomorfismo dato da (x,y,z) -> (x,y) con (x,y,z) in S² e z>=0.

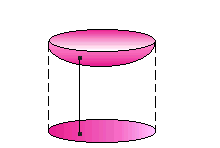
Possiamo quindi rappresentare P² come D²/~ con x ~ x' <==> x = x' oppure x, x' in S¹ sottoinsieme di D² e x = x'. Questa identificazione è rappresentata nella seguente figura:

Se togliamo da P² una piccola regione (omeomorfa all' interno di D²), ci resta un Nastro di Möbius.

Possiamo quindi pensare al piano proiettivo reale come ad un disco a cui sia stato aggiunto un Nastro di Möbius sul bordo.

Torniamo a confrontare Cilindro e Nastro.

Voglio dimostrare ora che il cilindro, C, non è omeomorfo al Nastro di Möbius, M, nonostante siano entrambi in qualche modo imparentati col rettangolo.
Osservazione: Il bordo di C è formato da due circonferenze, è quindi sconnesso. M invece gode di un altra particolarità: oltre ad avere un solo lato ha anche un solo bordo. Il bordo di M è connesso ed è omeomorfo ad una circonferenza.

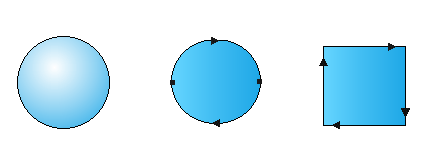
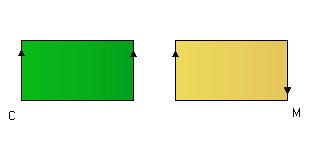
Dimostriamo ora che C non è omeomorfo a M. Per farlo ragioniamo per assurdo e supponiamo che C e M siano omeomorfi. Consideriamo sia C che M nella loro rappresentazione piana mediante un rettangolo con i lati identificati:

Considero m punto medio del lato verticale. Il punto m' che giace sul lato opposto e tale che m~m' è lo stesso sia per la relazione di equivalenza che porta al Cilindro, sia per quella che porta al Nastro. Cioè m' sarà il punto medio del lato verticale.

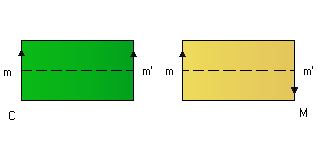
Tagliamo ora sia l'una che l'altra superficie lungo il segmento congiungente m e m', che indicherò con mm'. mm' taglia in due parti il cilindro, cioè lo sconnette. Ciò è facile da intuire, basti pensare al Cilindro in R³:

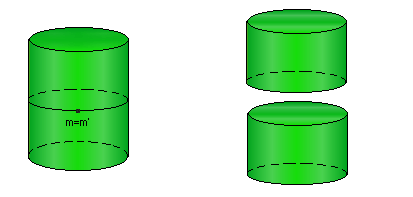
Il segmento mm' non taglia però il Nastro di Möbius, cioè M-mm' resta connesso. Infatti considero x,y in M giacenti entrambi sul rettangolo ma ai lati opposti del segmento mm'. Dal punto x posso arrivare al punto y con un arco, cioè senza fare salti. Ad esempio con il primo tratto di arco posso congiungere x ad A e con il secondo tratto congiungo A' ad y, dove A' è tale che A'~ A cioè A e A' rappresentano lo stesso punto sul Nastro, quindi ho ottenuto un unico arco congiungente x e y.

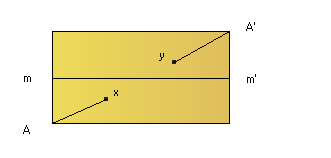
Quindi ho dimostrato che M-mm' è connesso per archi e quindi è connesso. Avevo supposto che C fosse connesso a M, sia f: M -> C. Considero g in M una curva di Jordan, per il teorema delle curve di Jordan anche f(g) è una curva di Jordan, quindi M-g deve essere omeomorfo a C-f(g). Ma se con g indico il segmento mm', ho che M-g è connesso mentre C-f(g) per quanto visto è sconnesso. Uno spazio connesso non può essere omeomorfo ad uno spazio sconnesso quindi M-g non può essere omeomorfo a C-f(g), allora M non è omeomorfo a C.

Il Cilindro ha una superficie interna e una esterna, cioè è orientabile, il Nastro di Möbius invece è una superficie non orientabile, cioè immaginiamo di voler dipingere con un pennello tale superficie. Ebbene riusciremmo a dipingerla totalmente senza staccare mai il pennello dalla superficie, cioè non si possono distinguere un interno ed un esterno.
Per convincerci meglio di quanto appena detto possiamo osservare questa animazione.

La superficie di Möbius, con le sue proprietà e con la sua particolare forma, è stata scelta da Escher come soggetto per alcune sue opere. Nel 1963 concluse Nastro di Möbius II, un capolavoro non solo rispetto le opere di questo genere ma rispetto tutta la sua produzione.

Osservando attentamente questa immagine ci si accorge che le formiche poste sulla superficie non stanno camminando su lati opposti, come potrebbe sembrare a prima vista. Al contrario esse proseguono una dietro l'altra in fila sull'unica faccia di quella superficie. Vediamo un altra immagine per accertarci di questo fatto.
Quest'opera è stata apprezzata anche per la dinamicità che comunica. Si tenga presente che nel momento in cui è nata non c'era ancora stato il boom delle animazioni al computer. Ma è curioso il fatto che proprio Nastro di Möbius II sia una delle prima immagine ad essere stata animata con Computer Graphics.

Una altra opera notevole sull'argomento è Nastro di Möbius I, questa volta non viene rappresentato semplicemente un Nastro di Möbius, ma quello che possiamo chiamare Bi-Nastro di Möbius. I serpenti infatti rappresentano quelo che succede ad una superficie come quella dell'opera con le formiche, quando la si taglia lungo una linea chiusa posta a distanza costante dal bordo. Abbiamo già osservato che tale taglio non sconnetterà la superficie, infatti se seguiamo i serpenti dell'immagine, vediamo che sono legati tra loro e si mordono la coda a vicenda. Mentre per costruire un Nastro di Möbius basta prendere una striscia di carta e incollarne gli estremi solo dopo aver compiuto un mezzo giro per uno di essi, per costruire un Bi-Nastro di Möobius prima di incollare i lati della striscia è necessario far compiere ad uno di essi due mezzi giri, cioè un giro completo. Lo stesso accade ai serpenti, ecco perché essi sembrano annodarsi due volte.