| 4.1 La critica di George Berkeley al calcolo infinitesimale (a cura di Ambra Catozzi) |
| Né nel calcolo differenziale di Leibniz né nel metodo
delle flussioni di Newton era esplicitamente illustrato il principio
secondo il quale una quantità infinitesima, sommata a una quantità
finita, può essere trascurata. Tale mancanza determinò una criticità
nella struttura del calcolo, evidenziando una abissale differenza
rispetto ai passaggi logici tradizionali. Alcuni eruditi del Settecento
si posero un interrogativo circa la nuova scoperta matematica: i
fondamenti del calcolo infinitesimale e la robustezza delle sue
procedure erano stati ben definiti? Molti scienziati furono ammaliati dalla potenza dei metodi infinitesimali, trascurando completamente il rigore dei nuovi procedimenti. Sicuramente la nuova branca della matematica si distanziava notevolmente dalla sistematicità tradizionale, cioè dai ragionamenti prettamente deduttivi, geometrici oppure induttivi. A mettere in evidenza la questione fu il filosofo George Berkeley, il quale sostenne che il successo del calcolo newtoniano fu soltanto frutto del caso, ossia il metodo delle flussioni risolveva certi problemi e trovava numerose applicazioni nel mondo reale esclusivamente grazie a una compensazione casuale di errori. Ovviamente, tutto ciò suscitò scalpore e polemiche che invasero il panorama erudito inglese. The Analyst: a Discourse addressed to an Infidel Mathematician Quest'opera venne pubblicata da George Berkeley nel 1734, il cui sottotitolo accenna all'argomento di discussione, ossia: "Viene esaminato se l'Oggetto, i Principi e le Inferenze dell'analisi moderna siano concepiti in modo più chiaro, o più evidentemente dedotti, rispetto ai Misteri Religiosi e ai Punti di Fede".  Il matematico infedele potrebbe coincidere con la figura di Edmond Halley, anche se altri ipotizzarono che potesse essere Isaac Newton. Unita a un taglio satirico, l'opera critica i fondamenti del calcolo infinitesimale ma non solo: Berkeley cercò infatti di smontare la matematica, affermò di scoprire numerosi vuoti nelle sue dimostrazione e nell'uso degli infinitesimi. Il fulcro della questione non era tanto deridere la matematica o i matematici, ma piuttosto dimostrare che gli scienziati, come i cristiani, ponevano alla base del loro ragionamento incomprensibili "misteri". Nel suo trattato, cercò di sostenere che, sebbene il calcolo portasse a risultati reali, le sue basi non erano più sicure di quelle della religione. Le osservazioni di Berkeley erano ben fondate e importanti in quanto focalizzavano l'attenzione dei matematici sull'esigenza di un chiarimento logico del calcolo; dunque, in qualche modo, Berkeley fu d'aiuto, perché sollecitò i matematici nella giusta direzione. Egli sviluppò un'ingegnosa teoria per motivare il fatto che la correttezza di un risultato del calcolo era frutto di due errori di compensazione. Analogamente ai fedeli cristiani e ai loro "misteri", Berkeley concluse che la certezza della matematica non era maggiore della certezza della religione. Esempi della debolezza del calcolo infinitesimale Berkeley centrò con molta precisione il principale punto debole della costruzione newtoniana, cioè la definizione di flussione, così come quella degli incrementi infinitesimi, data invece dai "matematici stranieri", ossia dai collaboratori di Leibniz. La seguente critica è contenuta nella XVI sezione del trattato ed è una delle più rilevanti; come si può notare, il tono e il registro della scrittura sono adatti e rivolti al "matematico infedele" (la traduzione è nostra). Se tu inizialmente assumi che una quantità sia aumentata di un valore nullo e, nell'espressione x+o, o non rappresenta nulla, in questa supposizione poiché non vi è incremento della radice, non ci sarà neppure incremento della potenza e di conseguenza, non comparirà nessuno dei termini della serie binomiale tranne il primo. Pertanto tu non arriverai mai legittimamente alla tua espressione di flussione con tale metodo. Quindi tu sei portato a procedere e a supporre in modo fallace un incremento (non nullo), modificando immediatamente dopo la tua supposizione in quella di incremento nullo. Può sembrare una grande abilità fare quest'ultima supposizione ad un certo momento, poiché se fosse stata fatta prima della divisione per o, tutto sarebbe svanito in una volta e non avresti ottenuto nulla. Con l'artificio di eseguire prima la divisione per o e poi cambiare l'ipotesi (cioè porre o=0) si conservano i termini 1 e n xn-1 , ma nonostante questo passaggio per coprire l'errore, questo resta. Infatti sia che si ipotizzi prima sia che si ipotizzi dopo, quando si pone o =0 in quello stesso istante la precedente ipotesi e tutto quello che si era ottenuto si elide. Questo è vero universalmente, qualunque sia il soggetto, in tutti i rami della conoscenza umana, in ciascuno dei quali io credo. L'uomo difficilmente ammetterebbe un ragionamento come questo che invece in matematica è accettato come dimostrazione. In poche parole, per calcolare la flussione di una funzione f(x) si deve infatti calcolare il rapporto incrementale  e porre e
= 0, ma, dividendo per e, si fa tacitamente l'ipotesi che e non sia
nullo e una volta effettuata la divisione non è lecito dunque, osservò
Berkeley, porre e = 0. Ciò era dovuto alla mancanza
di una precisa teoria dei limiti che rese difficile il superamento del
paradosso. L'altra definizione newtoniana, basata sulle prime e ultime ragioni, prevede invece la considerazione del rapporto non quando è uguale a zero, né quando è diverso da zero, ma nel momento stesso in cui si annulla e il triangolo caratteristico si contrae in un punto. Di questa formulazione ancora più oscura Berkeley si fa facilmente gioco nella XXXIV sezione: Si assume che le flussioni possono essere esposte o espresse da linee finite proporzionali ad esse: quali linee finite possono essere chiaramente concepite, conosciute e ragionate, in modo che possano essere sostituite con le flussioni e tali che le loro relazioni o proporzioni reciproche possano essere considerate come proporzioni di flussioni: con ciò la dottrina diventa chiara e utile. Io rispondo che se per arrivare a queste linee finite proporzionali alle Flussioni, si percorrono alcuni passaggi oscuri e inconcepibili, allora quelle stesse linee finite così chiaramente concepite, riconoscono che il tuo procedimento non è chiaro e che il tuo metodo non è scientifico. Ad esempio, si suppone che AB sia l'Ascissa, BC l'ordinata e VCH la tangente alla curva AC; sia Bb o CE l'incremento dell'ascissa, sia Ec l'incremento dell'ordinata che interseca VH nel punto T e sia Cc l'incremento della curva. La linea retta Cc prolungata fino a K, contiene tre piccoli triangoli: CEc rettangolo, CEc mistilineo e CET rettangolo. àˆ evidente che questi tre triangoli sono diversi l'uno dall'altro, il CEc rettangolo è minore del CEc mistilineo, i cui lati sono i tre incrementi menzionati precedentemente, e questo è minore del triangolo CET. Si suppone che l'ordinata bc trasli verso BC, in modo che il punto c coincida con il punto C; la linea retta CK, e di conseguenza la curva Cc, coincide con la tangente CH. Nel caso in cui il triangolo evanescente mistilineo CEc sarà , nella sua ultima forma, simile al triangolo CET: i suoi lati evanescenti CE, Ec e Cc saranno proporzionali a CE, ET e CT, i lati del triangolo CET. Quindi si conclude che le flussioni delle linee AB, BC e AC, essendo nell'ultimo rapporto dei loro incrementi evanescenti, sono proporzionali ai lati del triangolo CET o, che è tutt'uno, del triangolo VBC simile. àˆ stato in particolare sottolineato e insistito dal grande autore, che i punti C e c non devono essere distanti tra loro, con il minimo intervallo di tempo: ma questo, al fine di trovare le proporzioni definitive delle linee CE, Ec e Cc (cioè le proporzioni delle flussioni o velocità ) espresse in termini dei lati finiti del triangolo VBC, i punti C e c devono essere coincidenti. Questo è assolutamente inconcepibile. Eppure vi sono alcuni i quali mentre esprimono disappunto all'enunciazione di qualsiasi mistero, per quanto li concerne non fanno alcuna difficoltà , capaci di scolare un moscerino e di inghiottire un cammello 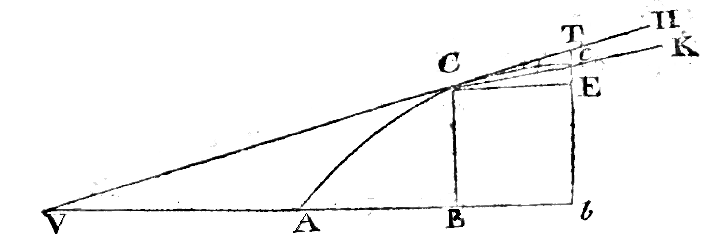 ... E che cosa sono queste flussioni? Le velocità di incrementi evanescenti. E che cosa sono questi incrementi evanescenti? Essi non sono quantità finite, non sono infinitesimi, non sono niente. E allora non dobbiamo forse chiamarli spettri di quantità defunte?  Risultati sorprendenti da principi precari Il filosofo irlandese non criticò sterilmente le fondamenta del calcolo infinitesimale, ma discusse e approfondì le motivazioni del successo di questa nuova branca della matematica. Moltissimi problemi infatti avevano trovato soluzione e, soprattutto, il corretto procedimento di risoluzione, grazie agli strumenti potenti del calcolo. Berkeley cercò di spiegare come da definizioni poco rigorose potessero discendere risultati tanto eccezionali, nascondendo una compensazione di errori. 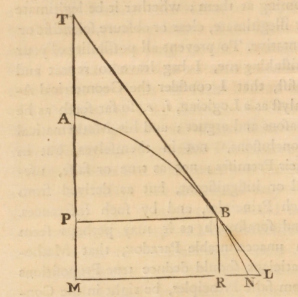 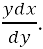 Ora, secondo Berkeley, si commette un primo
errore: il valore di PT risulta maggiore rispetto alla realtà :
effettivamente, non è il triangolo RNB che è simile a PTB, ma è RLB;
quindi (invece di RN) RL avrebbe dovuto essere il primo termine della
proporzione, cioè RN+NL, cioè dy+z, da cui la vera espressione della
sottotangente sarebbe stata 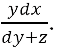 Si è quindi verificato un errore
per difetto nel rendere dy il divisore il cui errore era pari a z,
ossia il segmento NL compreso tra la curva e la tangente.
Ora per la natura della curva yy = px, supponendo che p sia il
parametro, da cui la regola delle differenze 
Ma se si moltiplica y+dy per se stesso e se si conserva l'intero
prodotto senza trascurare il quadrato della differenza, sostituendo le
quantità aumentate nell'equazione della curva si ha: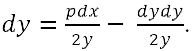 
Si è verificato un errore per eccesso nel rendere 
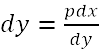che è seguito dall'errata regola delle differenze; la misura di questo
errore è 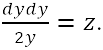 . Quindi i due errori essendo uguali e contrari si elidono: il primo errore per difetto è corretto dal secondo errore per eccesso. La mutua cancellazione dei due errori porta dunque a risultati esatti e si arriva "se non alla scienza, almeno alla verità ". L'opera si chiude con un elenco di 67 domande relative agli argomenti citati e discussi in precedenza. |
| 4.2 Il contributo di Bolzano al calcolo infinitesimale (a cura di Francesca Bonato) |
| Nell'opuscolo Rein analytischer Beweis des
Lehrsatzes, dass zwischen je zwey Werthen, die ein entgegengesetztes
Resultat gewà¤hren, wenigstens eine reelle Wurzel der Gleichung liege
del 1817 Bolzano dà una definizione di funzione continua in un
intervallo, che differisce poco da quella usata nella matematica
contemporanea: Dato un intervallo I = [𝑎,𝑏] e 𝑥 un punto interno ad 𝐼, 𝑓 è continua se la differenza 𝑓(𝑥+𝜔) − 𝑓(𝑥) può essere resa inferiore a qualsiasi valore dato prendendo 𝜔 sufficientemente piccolo. Inoltre definisce quella che oggi viene chiamata successione di Cauchy e dimostra che converge: Se in una successione di grandezze F1(x), F2(x), ... , Fn(x), ... , la differenza tra il termine ennesimo Fn(x) e ogni termine successivo Fn+1(x), lontano quanto si vuole dall'ennesimo, si mantiene più piccola di ogni grandezza data, prendendo 𝑛 sufficientemente grande, allora esiste sempre una certa grandezza costante ed una sola a cui si avvicinano sempre più i termini di questa successione e a cui si possono avvicinare tanto quanto si vuole prolungando la serie sufficientemente lontano. Il Teorema degli zeri, o Teorema di Bolzano, garantisce l’esistenza di almeno una radice nelle funzioni continue di variabile reale che assumono segni opposti ai due estremi di un intervallo. Una funzione continua di variabile 𝑥 che è positiva per qualche valore di 𝑥 e negativa per qualche altro valore di 𝑥 in un intervallo chiuso 𝑎 ≤ 𝑥 ≤ 𝑏 di continuità deve assumere il valore zero per un valore intermedio di 𝑥. cioè se 𝑓 è una funzione continua per 𝑥 che varia da 𝑎 a 𝑏, se 𝑓(𝑎)∙𝑓(𝑏) < 0, allora esiste almeno un valore 𝑐 tale che 𝑎 < 𝑐 <𝑏 e 𝑓(𝑐) = 0.  |
| 4.3 La compensazione degli errori di Carnot (a cura di Francesca Bonato) |
Nel 1797 Carnot pubblicò la famosa opera Réflexions
sur la métaphysique du calcul infinitésimal (Riflessioni
sulla metafisica del calcolo infinitesimale), in cui esamina i vari
approcci storici al calcolo infinitesimale, dall'antichità fino al
Sei-Settecento, cercando di dimostrare la necessità di una
compensazione degli errori per dare al calcolo una base sicura.
 Nell'opera Carnot ripercorre il dibattito sui fondamenti dell'analisi, sviscerando e confrontando le varie posizioni. Per Carnot il calcolo infinitesimale fornisce risultati corretti perché si possono compensare gli errori. Secondo Carnot gli infinitesimi sono quantità inapprezzabili introdotte unicamente per eseguire i calcoli che vengono eliminate quando si raggiunge il risultato finale. Gli infinitesimali invece sono quantità che hanno limite 0 o 1/0: nel primo caso si parla di quantità infinitamente piccole, nel secondo di infinitamente grandi. Per Carnot esistono due modi di trattare le variabili infinitamente piccole. Il primo si basa sull'attribuzione di valori effettivi alle variabili e il calcolo infinitesimale è allora «un calcolo degli errori compensati». Il secondo modo consiste invece nel considerare nulle tali variabili, e in tal caso l'analisi è un calcolo esatto, ma avente come oggetto delle quantità evanescenti. Poiché si ottengono gli stessi risultati con entrambi i metodi Carnot mira a riunirli per definire così un vero e proprio calcolo infinitesimale. Come funziona allora la compensazione degli errori? Se si introducono nel calcolo quantità infinitesimali per facilitare l'espressione delle condizioni del problema, inevitabilmente compariranno alcuni errori; questi errori però possono costantemente essere ridotti diminuendo il valore delle quantità inserite fino a eliminarle. Secondo Carnot è sempre possibile compensare l'errore, trascurando nel procedimento del calcolo la quantità infinitesimale che era stata introdotta e il fatto di trascurare queste quantità è assolutamente necessario per risolvere in modo corretto il problema. Quindi l'errore iniziale di inserire quantità indeterminate viene eliminato perché viene commesso un altro errore ossia quello di trascurare le quantità infinitamente piccole, in modo tale che i due errori si compensino. Il calcolo infinitesimale secondo Carnot è esatto e rigoroso perché gli errori vengono distrutti mediante il metodo di compensazione. Chiaramente se a una data quantità se ne sostituisce un'altra diversa risulterà un errore ma questo errore può essere minimizzato se la differenza fra le due quantità è piccola a piacere; quindi poiché gli errori si compensano a vicenda si ottiene ugualmente un risultato corretto. |
| 4.4 Cauchy: il calcolo diventa analisi (a cura di Jonathan Franceschi) |
| L'approccio di un matematico al calcolo infinitesimale
prima della fine del XVIII secolo è pragmatico: mira a risolvere
problemi soprattutto sperimentali, ispirati a situazioni reali
suggerite dai campi della fisica e dell'economia.
Lagrange è uno dei primi ad ammonire la comunità internazionale che la
mancanza di rigorose basi per il calcolo è una grande sfida per i
matematici
contemporanei. Dopo Cauchy, i fondamenti del calcolo diventano una
parte essenziale dell'analisi, passando da un calcolo del XVIII secolo
orientato ai
risultati e un calcolo del XIX secolo basato sul rigore dei risultati. Il calcolo di Cauchy Per il suo Cours d'analyse de l'ecole royale polytechnique. 1re partie: analyse algébrique (d'ora in avanti Cours d'analyse ) del 1821 Cauchy adottò come sottotitolo la frase di Lagrange "analyse algébrique". La vera innovazione è che, contrariamente a Lagrange, Cauchy comprese che fossero le disuguaglianze, invece delle uguaglianze, a poter essere la giusta base per il calcolo. Prima di Cauchy, le approssimazioni erano viste come un metodo per avvicinarsi sempre di più a un numero reale la cui esistenza era data per scontata. Dopo Cauchy, i numeri reali vennero definiti come limiti di processi approssimanti, e la loro esistenza venne dimostrata dalla convergenza dell'approssimazione. Quest'ultimo punto ci consente di osservare tre caratteristiche che le dimostrazioni di Cauchy avevano in comune. - Viene supposta implicitamente una forma dell'assioma di completezza dei numeri reali: l'esistenza di un limite finito per una successione monotona e limitata (questo è uno dei punti deboli del Cours d'analyse). - Vengono lasciati dei dettagli come esercizio per il lettore. - La dimostrazione si distingue per la sua notazione e la sua chiarezza. Limiti Il concetto di limite che propone Cauchy è: Quando i valori successivamente attribuiti alla stessa variabile si avvicinano indefinitamente a un valore costante, in modo che alla fine differiscano da questo di una quantità piccola a piacere, allora esso è chiamato il limite di tutti gli altri. Non compaiono concetti geometrici nè fisici. Nonostante la formulazione sia puramente verbale, la forte componente d'innovazione è che questa definizione si può convertire in termini di disuguaglianze e Cauchy sfrutterà questo fatto nelle dimostrazioni dei teoremi. Tra l'altro, Cauchy è il primo che introduce la possibilità che il rapporto tra due quantità che vanno a zero possa convergere a un limite, mentre i matematici prima di lui davano per scontato che ciò accadesse, occupandosi direttamente di studiare i metodi per calcolare tale limite. Questo si apprezza notevolmente con la buona definizione di derivata, che si utilizza tuttora: la derivata è definita come il limite del rapporto Δy / Δx, quando esso esiste. Continuità Fino alla prima metà del Settecento, i matematici trattavano quasi esclusivamente funzioni polinomiali, razionali, trigonometriche ed esponenziali; ciò faceva sì che non si avvertisse la necessità di una nozione rigorosa di continuità . Questo cambiò quando si cominciò a studiare equazione differenziali, che potevano avere come soluzioni anche delle funzioni che non fossero esprimibili in termini di funzioni elementari. All'inizio del 1800 sia Cauchy (1821) che Bolzano (Rein analytischer Beweis des Lehrsatzes dass zwischen je zwey [sic] Werthen, die ein entgegengesetztes Resultat gewaehren, weningstens eine reele Wurzel der Gleichung liege, 1817) diedero la prima definizione rigorosa di funzione continua. Quella di Cauchy è composta da due parti: nella prima il linguaggio è quello dell'algebra delle disuguaglianze, fondamentale per il rigore dell'impostazione. Nella seconda il linguaggio è quello degli infinitesimali, per dare al lettore un'idea intuitiva della continuità : La funzione f(x) è una funzione continua della variabile x tra due limiti [dove limiti sta per estremi di un intervallo] se, per ogni valore di x tra quei limiti, la differenza [in modulo] f(x+α) - f(x) decresce indefinitamente con α. In altre, parole, la funzione f(x) è continua rispetto a x tra gli estremi dati se, tra questi limiti, un incremento infinitamente piccolo nella variabile produce sempre un incremento infinitamente piccolo nella funzione stessa. Il risultato più significativo sulle funzioni continue dimostrato per la prima volta da Cauchy nel Cours d'analyse è senza dubbio il teorema dei valori intermedi (o degli zeri). Teorema. Sia f(x) una funzione reale della variabile x, continua rispetto a tale variabile tra x = x0 , x = X. Se le due quantità f(x0), f(X) hanno segno opposto, l'equazione (1) f(x) = 0 può essere soddisfatta da uno o più valori reali di x [compresi] tra x0 e X. Convergenza Lungo il corso del Settecento, la nozione di convergenza di una serie non era univoca. Spesso, infatti, una serie era definita convergente se il suo termine n-esimo tendeva a zero, altre volte la definizione di convergenza era analoga a quella contemporanea. Nel 1821 Cauchy diede la definizione moderna di convergenza e di somma di una serie con termini u0 , u1 , u2 , ...: Sia sn = u0 + u1 + ... + un-1 la somma dei primi n termini, con n qualunque intero. Se, per crescenti valori di n la somma sntende a un certo limite s, la serie sarà chiamata convergente e il limite in questione sarà chiamato la somma della serie. Inoltre Cauchy espose il criterio omonimo per la convergenza delle serie nel Cours d'analyse, ma Bolzano lo anticipò nel 1817, dando una sua versione del criterio, anche se non si può concludere che la definizione di Cauchy debba necessariamente essere dipesa da quella di Bolzano. Il criterio di Cauchy afferma che la serie di termine generale un converge (secondo la definizione precedente) se e solo se, per ogni K reale, le differenze tra la prima e le successive somme parziali sono inferiori a K per n abbastanza grande: sn+2 - sn= un + un+1 (2) sn+3 - sn= un + un+1 + un+2 ... Vale la pena aggiungere che il concetto di convergenza introdotto da Cauchy e Bolzano mancava di alcune sfumature moderne, in particolare Cauchy non faceva distinzione tra convergenza puntuale e convergenza uniforme: spesso sottintendendo quest'ultima in dimostrazioni che, in effetti, richiedevano l'uniformità . È famoso ad esempio il risultato, errato, che il limite di una successione di funzioni continue sia continuo, pubblicato da Cauchy nel 1821 e contestato nel 1826 da Abel, con un controesempio costruito nel contesto delle serie di Fourier. Questo fatto contribuì a porre l'attenzione sulla necessità di distinguere i diversi tipi di convergenza nell'ambito dell'analisi reale e funzionale. Derivate Mentre i protagonisti del Cours d'analyse sono i limiti, la continuità e la teoria della convergenza delle serie, le basi del moderno calcolo differenziale e integrali vengono gettate due anni dopo. Cauchy, nel Calcul infinitésimal del 1823 definì per la prima volta la derivata di una funzione in termini moderni, come limite del rapporto incrementale (quindi di un quoziente di differenze):  Questo limite, quando esiste, ha un valore definito per ogni particolare valore di x; ma varia con x ... [Sarà ] una nuova funzione della variabile x ... Per indicare questa dipendenza, diamo alla nuova funzione il nome di funzione derivata, e la denotiamo con l'aiuto di un accento, con la notazione y' o f '(x). Cauchy è il primo matematico a dimostrare teoremi usando una definizione rigorosa di derivata, per esempio il teorema del valor medio per funzioni differenziabili, che è una conseguenza della proprietà (espressa in termini moderni)  dove f è differenziabile in (x0 , X) e continua in [x0 , X]. Questo è anche il primo teorema in cui compare la notazione epsilon-delta che si è affermata fino ai giorni nostri. Integrali L'idea di Cauchy fu quella di considerare una funzione f(x) continua su un intervallo (x0 , X) e di suddividere l'intervallo in n sotto-intervalli (xi , xi+1), non necessariamente uguali tra loro. A questo punto l'integrale poteva essere approssimato semplicemente sommando gli n prodotti (xi+1 - xi ) f(xi). Il problema di questo approccio è che il valore dell'approssimazione dipende dalla suddivisione dell'intervallo, quindi, affinché la definizione fosse ben posta, era necessario dimostrare che in ultima analisi il valore del limite di tale approssimazione fosse indipendente dalla suddivisione. Cauchy riuscì nell'intento usando una versione di continuità della funzione f(x) più forte di quella puntuale, che ora chiamiamo continuità uniforme.  Il risultato più importante sugli integrali definiti è certamente quello che ora è conosciuto come il teorema fondamentale del calcolo integrale, che Cauchy dimostrò ispirandosi nuovamente a Lagrange, che, anche senza una teoria consistente sull'integrale come quella di Cauchy, era riuscito a provare - di nuovo considerando espansioni in serie di Taylor - che se si considera una funzione F(x) definita come l'area sotto il grafico della curva y = f(x) nell'intervallo (x0 , x), allora vale che f(x) = F '(x). Conclusione Dunque perché il lavoro di Cauchy è importante? Prima, l'analisi era una branca in forte espansione, vitale, che ben si adattava alle esigenze anche pragmatiche della nuova classe protagonista in Europa, la medio-borghesia. I passi che si muovevano in questo nuovo territorio erano veloci, certo, ma anche incerti: abbiamo ricordato all'inizio l'imbarazzo dei matematici della seconda metà del Settecento nel giustificare le proprie procedure. Le fondamenta che potessero sorreggere questo nuovo edificio erano senz'altro intuite, ma senza di esse i risultati che il calcolo produceva erano mattoni isolati. Cauchy non ha solamente proposto definizioni nuove o dimostrato nuovi teoremi: Cauchy ha costruito un'impalcatura. Cauchy infatti non ha certo completato l’opera di rigorizzazione del calcolo - tanto meno l’ha iniziata - però ha dato gli strumenti per costruire risultati ben più generali di quelli considerati fino ad allora. Le successioni di Cauchy furono adottate per esempio come punto di partenza per una definizione rigorosa dei numeri reali prima di Dedekind, e sono uno strumento fondamentale dell’analisi in spazi di dimensione infinita; la definizione di integrale proposta da Riemann è una conseguenza quasi naturale della proposta di Cauchy di integrale come somma di aree di rettangoli. Sono solo due degli esempi di ciò che il lavoro di Cauchy ha permesso di raggiungere. Cauchy ha anche avuto il grande merito di riconoscere che l'algebra potesse essere il punto di partenza giusto per il calcolo, così come aveva fatto Lagrange prima di lui, ma a differenza di questi Cauchy ha saputo indicarne i limiti, ovvero dare delle condizioni secondo le quali certi procedimenti erano permessi. Riuscire a dotare l'algebra del calcolo, così comoda e operativa, dello stesso rigore, e dunque degna dello stesso rispetto della geometria degli antichi Greci, ha certamente dato un'enorme spinta a questa giovane branca della matematica. I metodi che Cauchy ha proposto sono essenzialmente quelli che vengono tuttora usati e insegnati nelle scuole e nelle università , anche perché sono scevri da speculazioni filosofiche o da intuizioni fisiche: sono pratici, asciutti, vanno all'essenza del problema che devono studiare proprio perché chi li ha introdotti ha colto quali fossero i punti essenziali attorno cui costruire tutto il resto. Insomma, Cauchy è stato la tessera fondamentale nel passaggio dal calcolo di Newton e Leibniz alla moderna analisi matematica. |