Bolla Capire il mondo attraverso una bolla
un percorso di scienze integrate tra schiume e bolle di sapone
 
  Home Premessa Cenni storici Percorso Approfondimenti Fonti  
  INTRODUZIONE  |  PROBLEMI DI GEOMETRIA  |  PROBLEMI DI FISICA            
 

Quando si affronta lo studio delle relazioni fra grandezze, ad esempio peso e altezza delle persone, temperatura e altitudine, lunghezza della circonferenza e il suo raggio, forza applicata ad una molla e relativo allungamento, può essere necessario far comprendere agli studenti che nella rappresentazione grafica dei dati raccolti, si ottiene un diagramma i cui punti sono "sparsi" ma vicini ad una curva.

Come fare per individuare la curva che approssima il più possibile il diagramma a dispersione? Esiste un metodo detto dei minimi quadrati che viene di seguito illustrato considerando come esempio la relazione fra forza applicata ad una molla e il suo allungamento.

Si procede con la raccolta dei dati.

Forza (in newton) Allungamento (in cm)
1 3
2 4
3 5.5
4 7
5 9.5
6 12


Si trasferiscono i risultati analiticamente in un sistema di riferimento cartesiano ortogonale, ottenendo i punti:
A(1 ; 3)    B( 2 ; 4)    C (3 ; 5.5)    D ( 4 ; 7)    E ( 5 ; 9.5)    F ( 6 ; 12 )

e il conseguente diagramma: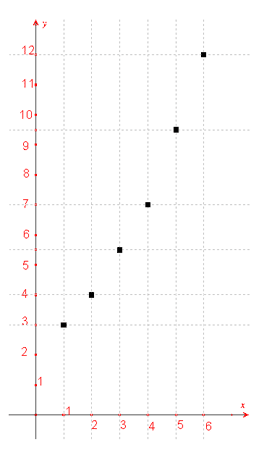

Retta regressione

Osservato che tali punti non risultano allineati, possiamo chiederci se esiste una retta che passa "vicino" ad essi.

Indicata con y = mx + q l’equazione della retta generica, si nota che accanto ai valori effettivi rilevati esistono allora dei valori teorici. Precisamente

y(1) = m + q
y(2) = 2m + q
y(3) = 3m + q
y(4) = 4m + q
y(5) = 5m + q
y(6) = 6m + q

Consideriamo il quadrato degli scarti tra i valori teorici e i valori misurati:

(y(1) - 3)2 = (m + q – 3)2 = m2 + q2 + 9 + 2mq – 6m – 6q

(y(2) - 4)2 = (2m + q – 4)2 = 4m2 + q2 + 16+ 4mq – 16m - 8q

(y(3)- 5.5)2 = (3m + q – 5.5)2 = 9m2 + q2 + 30.25 + 6mq – 33m – 11q

(y(4)- 7)2 = (4m + q + 7 )2 = 16m2 + q2 + 49 + 8mq – 56m – 14q

(y(5)- 9.5)2 = (5m + q – 9.5)2 = 25m2 + q2 + 90.25 + 10mq – 95m – 19q

(y(6)- 12)2 = (6m + q – 12)2 = 36m2 + q2 + 144 + 12mq – 144m – 24q

Sommando si ottiene

S = m2 + q2 + 9 + 2mq – 6m – 6q + 4m2+ q2 + 16 + 4mq – 16m - 8q + 9m2 + q2 + 30.25 + 6mq – 33m - 11q + 16m2 + q2 + 49 + 8mq – 56m – 14q + 25 m2 + q2 + 90.25 + 10mq – 95m – 19q + 36m2 + q2 + 144 + 12mq – 144m – 24q

Sommando i termini simili

S = 91 m2 + 6 q2 + 338.5 + 42mq – 350m – 82q

Determiniamo i valori di m e q che rendono minima la somma:

Se consideriamo q costante, otteniamo l’equazione di una parabola con la concavità verso l’alto e perciò dotata di minimo in corrispondenza all’ascissa del vertice:

S = 91 m2 + m(42q – 350) + (6q2 + 338.5 – 82q )

m = (175 – 21q) / 91

Da m costante si ottiene

S= 6q2 + q(42m – 82) + (91m2 - 350m + 338.5)

che è l’equazione di una parabola con concavità verso l’alto. Esiste perciò un minimo assoluto in corrispondenza al valore dell’ascissa

q = (41 – 21m) / 6.

Risolvendo il sistema:

91 m = 175 – 21q
6q = 41 – 21m
si ottiene m = 63/35 e q = 8/15

Si ottiene la retta di equazione y = (63/35) x + 8/15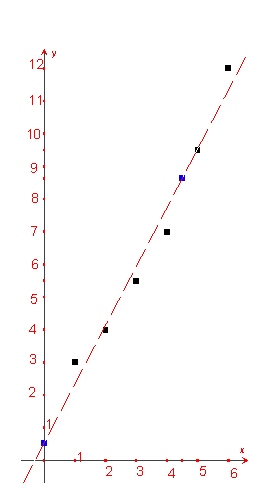

Retta regressione

La retta ottenuta viene chiamata retta di regressione.
Tale retta non passa per nessuno dei punti, ma "vicino" ad essi.

Va osservato che il metodo dei minimi quadrati può essere utilizzato anche per modelli non lineari; in tal caso la somma non è più traducibile in una equazione di secondo grado ma di ordine superiore, e i calcoli richiesti risultano più complessi.