 |
Capire il mondo attraverso una bolla un percorso di scienze integrate tra schiume e bolle di sapone |
|
|||||||||
| Home | Premessa | Cenni storici | Percorso | Approfondimenti | Fonti | ||||
| INTRODUZIONE | PROBLEMI DI GEOMETRIA | PROBLEMI DI FISICA | |||||||||
|
Prima di procedere alla ricerca dei massimi e dei minimi, va dimostrata la loro esistenza: per i casi che analizziamo è sufficiente porre il problema dell’esistenza per funzioni reali in una reale. In tal caso la trattazione si basa sui seguenti teoremi: Teorema 1 (di Weierstrass). Se f(x) è una funzione continua su un intervallo [a,b] allora esistono il massimo e il minimo dei valori di f(x). Un teorema analogo vale per una funzione a più variabili continua su un insieme di punti limitato e chiuso. Qualora la funzione f(x) sia continua su un dominio che non sia un intervallo chiuso e limitato, il teorema di Weierstrass non può essere usato per garantire l’esistenza di valori massimo e minimo di f. Ma f può avere ugualmente valori di questo tipo. Il teorema seguente costituisce un adattamento del teorema 1 per studiare alcuni casi di funzioni continue su intervalli infiniti o aperti. Teorema 2. Se f(x) è una funzione continua sull’intervallo aperto (a,b) e se f converge a L per x tendente ad a+ e se f converge a M per x tendente a b- allora valgono le seguenti conclusioni: i) Se f(u) > L e f(u) > M per qualche u di (a,b) allora f ha un massimo assoluto in (a,b) ii) Se f(v) < L e f(v) < M per qualche v di (a,b) allora f ha un minimo assoluto in (a,b) In questo teorema a può essere "meno infinito" e b può essere "più infinito". Analizziamo ora alcuni teoremi di massimo e di minimo che si possono studiare a livello elementare con un approccio di tipo algebrico o sintetico. Le proposizioni: 1) Tra tutti i rettangoli di dato perimetro il quadrato ha l’area massima 2) Tra tutti i rettangoli di data area il quadrato ha il perimetro minimo sono ottenute l’una dall’altra scambiando le parole perimetro e area e i termini massimo e minimo (per questo vengono chiamate duali o reciproche). Prima di procedere alla loro dimostrazione credo sia opportuno da un punto di vista didattico, per questo semplice caso, far vedere direttamente che le proposizioni 1) e 2) sono equivalenti (senza applicare il principio di dualità, che tratteremo in seguito) riservandoci di far riferimento a quest’ultimo (o ad altri principi) in situazioni complesse. Facciamo vedere l’equivalenza dei problemi 1 e 2: dato 1) e considerati i rettangoli di area fissata allora il quadrato Q fra essi ha il perimetro minimo. Ragionando per assurdo, se il quadrato Q non fosse tra i rettangoli ad esso equivalenti quello di perimetro minimo allora esisterebbe un rettangolo R (non quadrato) ad esso equivalente con perimetro * 2p < 2P (perimetro di Q).D’altra parte tra tutti i rettangoli di perimetro 2p in base alla proposizione 1 esiste un quadrato Q’ di area massima. Si perviene perciò al seguente risultato: R e Q’ sono isoperimetrici di perimetro 2p e l’area di R = area di Q < area di Q’. Ne viene che il perimetro di Q risulta minore del perimetro di Q’, cioè 2P < 2p. Questo risultato è in contraddizione con *. Pertanto siamo arrivati all’assurdo, per cui risulta che Q ha perimetro minimo tra tutti i rettangoli di fissata area. Viceversa facciamo vedere che Dato 2) e considerati i rettangoli di perimetro fissato allora il quadrato ha area massima. Ragioniamo per assurdo supponendo che il quadrato Q non abbia area massima fra tutti i rettangoli di perimetro dato 2P: esisterebbe allora un rettangolo R (non quadrato) con lo stesso perimetro di Q suvvalente Q, cioè ** area di R > area di Q.D’altra parte sia A = area di R: per la proposizione 2) fra i rettangoli di area A ,il quadrato Q’ ha perimetro minimo. Segue che 2p(perimetro di Q’) < 2P(perimetro di R) = perimetro di Q.Ne viene che area Q’ = area R < area Q. Questo risultato è in contraddizione con **. Si è giunto a questo assurdo avendo supposto che fra tutti i rettangoli di perimetro fissato il quadrato non abbia area massima, per cui vale la tesi. Dimostriamo Problema 1: Fra tutti i rettangoli di dato perimetro il quadrato ha l’area massima.  Dimostrazione Indichiamo con p - x e con p + x le misure dei lati dei rettangoli isoperimetrici di perimetro 4p.  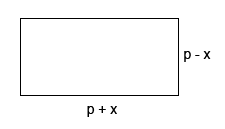Ne consegue che l’area dei rettangoli risulta funzione di x e vale A( x) = ( p – x) (p + x)= p2 – x2 con x in [a,p]: per il teorema di Wierstrass questa funzione ha massimo sull’intervallo considerato: in particolare l’area risulta massima se x vale zero e cioè nel caso del quadrato. Si nota che il minimo di A(x) è ottenuto nel caso in cui x sia p. Per l’equivalenza dimostrata vale anche il teorema Problema 2: Fra tutti i rettangoli di fissata area il quadrato ha perimetro minimo. Diamo anche una dimostrazione diretta Consideriamo i rettangoli di fissata area A2 dove A x e A/x rappresentano le dimensioni del generico rettangolo con x > 0. Consideriamo la funzione semiperimetro P(x)=A x + A/x con x positivo. Ne viene che P(x) = A( x2 +1)/x = A ( 2 + (x-1)2/x) Il rettangolo di perimetro minimo si ottiene nel caso in cui la somma è minima, cioè per x= 1. Si tratta perciò del quadrato. In questo caso non c’è massimo. Si noti che trattandosi di una funzione continua su un insieme aperto non vale il teorema di Weierstrass. In algebra i teoremi precedenti si traducono nei seguenti teoremi: Il prodotto di due numeri reali la cui somma è costante è massimo quando i due numeri sono uguali fra loro. Reciprocamente: la somma di due numeri positivi il cui prodotto è costante è minima quando i due numeri sono uguali fra loro. Consideriamo ora un problema storico. Problema 3: Fissati la retta r e i punti A e B distinti, individuare un punto C sulla retta in modo che la spezzata ACB abbia lunghezza minima (problema di Erone) Dimostrazione: Si noti che qualora i punti A e B appartengano alla retta r o appartengano ai semipiani opposti rispetto a r il risultato è immediato. Il problema è significativo qualora i punti A e B appartengano allo stesso semipiano rispetto alla retta r ,come illustrato in figura.  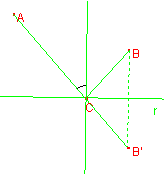Si consideri il punto B’ simmetrico di B rispetto alla retta r: sia C il punto della retta r e del segmento AB’. Si nota che per la simmetria assiale di asse r, CB è congruente a CB’, per cui la spezzata ACB è congruente al segmento AB’. Del resto ogni altro cammino che congiunga A con B passando per un qualsiasi altro punto X della retta r distinto da C fornisce una spezzata AXB congruente ad AXB’ ,che a sua volta è di lunghezza maggiore del segmento AB’(infatti nel triangolo AXB il lato AB’ è minore della somma degli altri due lati ). Nota: questo risultato si può tradurre in altro modo evidenziando l’aspetto fisico dell’ottica geometrica, noto come principio di riflessione. Dimostriamo ora il Problema 4: Tra i triangoli equivalenti di base fissata quello di perimetro minimo è il triangolo isoscele. 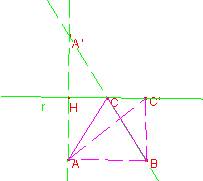Dimostrazione:  Fissata la base AB, tutti i triangoli equivalenti devono avere la stessa altezza: sia ABC’ uno dei triangoli ed r la retta per C’ parallela alla base. I triangoli di base AB e con il terzo vertice appartenente alla retta r sono tra loro equivalenti. Per rendere minimo il perimetro potremo individuare il punto C con la costruzione del problema di Erone. Costruito il triangolo ABC, dimostriamo che è isoscele: infatti, detto H il punto di intersezione tra AA’ e la retta r, esso risulta essere il punto medio del segmento AA’ e quindi C è il punto medio di A’B. Inoltre HC è la metà della base AB. Detto M il punto medio della base la retta CM è parallela a AA’ e quindi perpendicolare alla base. Ma allora nel triangolo la mediana è altezza per cui il triangolo è isoscele. Segue il Problema 5: Fra tutti i triangoli equivalenti il triangolo di perimetro minimo è quello equilatero. Dimostrazione: Per il teorema precedente fissata una base il triangolo di perimetro minimo è quello isoscele e perciò cambiando base si ottiene ancora un triangolo isoscele e quindi equilatero. Per casi piu’ complessi conviene utilizzare il "Principio di dualità (o di reciprocità)". Principio di dualità (o di reciprocità) Data una corrispondenza tra due variabili x, y se per ogni valore a di x i valori corrispondenti di y ammettono un massimo (o un minimo ) b che cresce al crescere di a, allora a è il minimo (o rispettivamente il massimo) dei valori di x che corrispondono ad y = b Non dimostriamo questo teorema e rimandiamo per un approfondimento a [5],[6]. In base al Principio di Dualità valgono i teoremi duali: Problema 6-7:
|