
Dalla costruzione risulta direttamente che la proiezione di Mercatore è conforme. La proiezione di Mercatore ha anche la proprietà di trasformare le lossodromie in rette
![]()
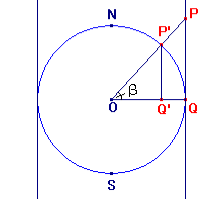
La proiezione di Mercatore è una delle proiezioni che consentono di rappresentare i paralleli ed i meridiani mediante un reticolato cartesiano di rette tra di loro ortogonali. Fondamentalmente tutte le rappresentazioni di questo tipo si basano sull'osservazione che si può proiettare la superficie terrestre dal suo centro su un cilindro ad essa circoscritto, dopodiché basta tagliare il cilindro lungo una sua generatrice e considerarne lo sviluppo su di un piano. Le equazioni di tale proiezione sono:

Dalla costruzione risulta direttamente che la proiezione di Mercatore è conforme. La proiezione di Mercatore ha anche la proprietà di trasformare le lossodromie in rette |
|
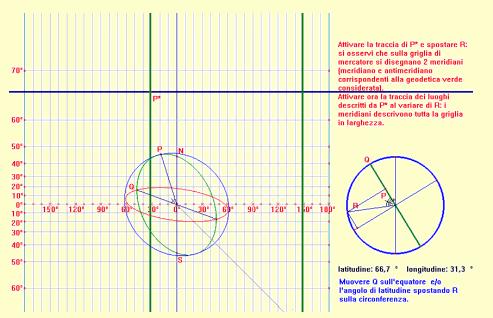
(clicca qui per aprire l’immagine interattiva)
Osservazione. Come illustrato in figura, l'equatore (β=0) diventa sulla carta l'asse delle x; un meridiano, assunto come fondamentale (λ=0) l'asse delle y; i meridiani sono rette parallele di equazione x=rλ, le cui distanze sono proporzionali alle differenze di longitudine; quindi a meridiani «equidistanti» sulla sfera corrispondono rette equidistanti sulla carta. Anche i paralleli sono rette parallele all'asse delle ascisse, la cui distanza cresce al crescere di β dall'equatore ai poli; il polo Nord ed il polo Sud non hanno immagine sul piano (intuitivamente il polo Nord corrisponde ai punti di ordinata +∞; il polo Sud ai punti di ordinata -∞).