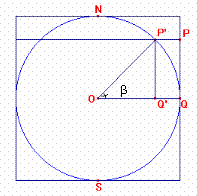
La proiezione di Lambert fa parte anch'essa delle proiezioni che consentono di rappresentare i paralleli ed i meridiani mediante un reticolato cartesiano di rette tra loro ortogonali. In questo caso, però, ci si propone di ottenere una proiezione equivalente. Eccone la costruzione: dopo aver circoscritto alla superficie terrestre un cilindro, si considera il piano parallelo al piano equatoriale e passante per un punto qualsiasi P’ della sfera e il semipiano per l'asse polare che contiene il meridiano passante per P’. Questi determinano una retta che interseca il cilindro in un punto P, che diremo l'immagine di P’; allora le equazioni di questa applicazione, come è evidente dalla prima figura, risulteranno:

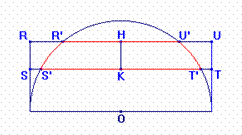
Come già detto, questa proiezione è equivalente, cioè conserva le aree: è noto, infatti, che la superficie di ogni zona sferica R’S’T’U’ è uguale a quella laterale del corrispondente cilindro RSTU.

 L'applicazione di Lambert non è conforme ma è equivalente.

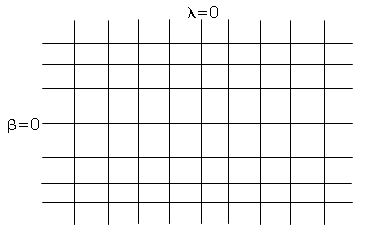
Osservazione. Ai meridiani corrispondono rette parallele all'asse y, che stanno tra di loro a distanze proporzionali alle differenze di longitudini; ai paralleli, rette parallele all'asse x, le cui distanze diminuiscono al crescere di β.