Clicca qui per aprire l’immagine interattiva

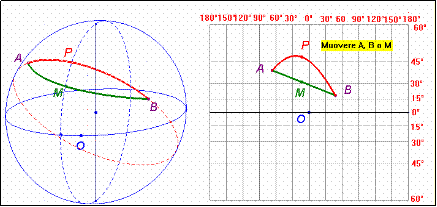
Le lossodromie sono quelle curve che formano un angolo costante con i meridiani della sfera; a parte i paralleli, perpendicolari ai meridiani, le lossodromie formano sulla superficie delle spirali che tendono asintoticamente ai poli. Per dimostrare che le lossodromie vengono trasformate in rette, basta osservare che, essendo la proiezione di Mercatore conforme, la linea piana corrispondente alla lossodromia sulla carta deve incontrare sotto angolo costante i meridiani, rappresentati da rette tra loro parallele, e dunque è una retta. Nella figura a fianco osserviamo la rappresentazione sulla sfera terrestre e sulla carta di Mercatore della lossodromia in verde e dell’ortodromia (arco di cerchio massimo) in rosso.

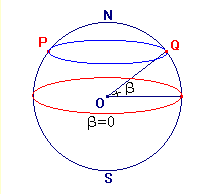
In virtù di questa proprietà, la proiezione di Mercatore è particolarmente utile per la navigazione marittima: infatti, volendo dirigere la nave da un punto P ad un punto Q, basterà segnare sulla carta l'immagine della lossodromia, cioè tracciare la retta che unisce i trasformati dei punti P e Q, misurare l'angolo che essa forma con i meridiani (angolo di rotta) e dirigere la nave nella direziono PQ, mantenendo costantemente fisso l'angolo sulla bussola. Si osservi (vedi figura a lato) che però, in questo modo, si utilizza non il cammino più corto tra due punti, ma quello di direzione costante. Infatti la proiezione di Mercatore non conserva le geodetiche; per esempio, dati due punti P e Q sulla sfera, non appartenenti all'equatore, con la medesima latitudine e longitudini che differiscano di 180°, la lossodromia per P e Q è l'arco di parallelo che li unisce, mentre la geodetica per P e Q è l'arco di cerchio massimo, passante per il polo dell'emisfero a cui appartengono P e Q .