Gaspard Monge, Géométrie descriptive, 1a ed. 1794-95. 6a ed. 1837

Gaspard Monge è considerato l'iniziatore della geometria pura moderna. Monge fu tra i fondatori dell'École Politecnique, una delle strutture educative (dedicate all'istruzione superiore) sorte dalla Rivoluzione Francese. Un insegnamento nuovo introdotto da Monge fu quello della geometria descrittiva. L'opera di Monge, Géométrie Descriptive  (1794-95), raccoglie le lezioni tenute  all'École Normale dell'anno terzo. Contiene il metodo della doppia proiezione ortogonale, ossia il metodo ancora in uso nel disegno geometrico, per cui da due proiezioni su due piani ortogonali (pianta e alzata), uno dei quali ribaltato sull'altro, si ottengono le proprietà della figura spaziale e viceversa.

L'insegnamento di Monge all'École Politecnique formò nuove generazioni di ingegneri e stimolò la rinascita della geometria sintetica che ebbe uno sviluppo straordinario nella prima metà dell'Ottocento.

Il teorema di Monge qui riportato è un esempio in cui la dimostrazione di un teorema di geometria piana è più semplice facendo uso della geometria dello spazio.

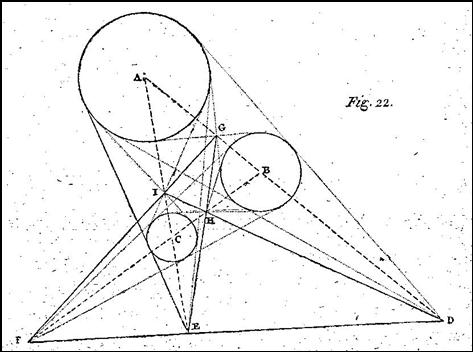
Tre cerchi qualunque del piano considerati a due a due hanno le tangenti comuni che si incontrano in tre punti allineati.