Annibale Giordano (1769-1859)

Annibale Giordano, allievo a Napoli di Nicola Fergola, risolse sinteticamente il problema (1788):

Dato un cerchio e n punti del suo piano, inscrivere in tale cerchio un poligono i cui lati, eventualmente prolungati, passino, secondo un certo ordine, per i punti dati.

Nel caso in cui n=3 e i punti dati siano allineati, il problema si riduce ad un problema risolto da Pappo nel libro VII della sua Collezione matematica, proposizione 117.

Sempre per 3 punti ma comunque disposti nel piano, il problema fu proposto da Cramer a Castillon e da lui risolto nel 1776.

Altre costruzioni più semplici furono date da Eulero e da Fuss (1783).

Annibale Giordano nel 1788 risolse per via sintetica il problema nel caso generale di n punti qualunque. Un'altra soluzione sintetica venne proposta da Gianfrancesco Malfatti lo stesso anno.

Vediamo la soluzione di Pappo ed una sua costruzione realizzata con Cabri.

Pappo utilizza il metodo dell'analisi che egli stesso spiega in questo modo: "Nell'analisi viene ammesso ciò che si cerca per arrivare, sviluppando le conseguenze, alla sintesi di quello che era stato ammesso". In altri termini l'analisi è come una "soluzione alla rovescia" in cui  supponendo il problema risolto e ritornando sui propri passi si arriva ad una proprietà che consente poi di determinare la costruzione dell'oggetto cercato.

All'inizio del libro VII elenca e descrive diverse opere che utilizzano questo metodo: i Dati, i Porismi e i Luoghi  superficiali di Euclide, tutte le opere di Apollonio in gran parte perdute (la Sezione di un rapporto, la Sezione di un'area, la Sezione determinata, le Inclinazioni, i Luoghi piani, i Contatti, le Coniche), i Luoghi solidi di Aristeo e Sulle medie di Eratostene.

Il teorema di Pappo in questione (Collezione Matematica VII, 117) fa riferimento al primo libro dell'opera perduta di Apollonio, i Contatti e utilizza le proposizioni 105, 107-109 del medesimo libro VII .

Supponiamo per semplicità che i punti siano esterni al cerchio, il problema può enunciarsi come segue:

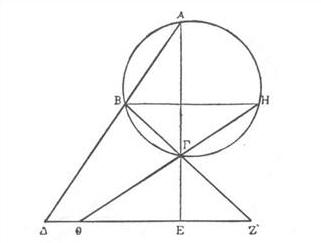
Dato un cerchio e tre punti D, E, Z allineati, determinare un punto A sulla circonferenza tale che, dette B e G le intersezioni di AD e AE con la circonferenza, il punto B stia sul prolungamento di GZ.

Soluzione di Pappo: Seguendo il metodo dell'analisi, supponiamo noto il triangolo ABG soluzione del problema. Conducendo dal punto B la retta BH parallela alla retta dei punti dati, la retta HG interseca la retta DEZ in un punto T di cui è nota la posizione, infatti per il parallelismo delle rette BH e DZ, l'angolo BHG è uguale all'angolo HTZ, a sua volta uguale all'angolo BAG in quanto angoli alla circonferenza che sottendono il medesimo arco BG. Ne segue che i triangoli ADE e TGE sono simili e quindi sussiste la proporzionalità tra i lati AE : TE=DE:GE, ossia AE·GE=TE·DE. Essendo il prodotto AE·GE uguale al quadrato della tangente condotta dal punto E al cerchio ABG, esso non dipende dal punto A ma solo dai dati del problema. Pertanto risulta determinato anche il segmento TE e quindi la posizione di T.

Ora il problema è ricondotto al seguente: dati un cerchio e due punti (esterni) T e Z, determinare il punto G sulla circonferenza tale che, dette B e H le intersezioni delle semirette TG e ZG con la circonferenza, la retta BH risulti parallela alla TZ (Collezione matematica VII, 105).

Procedendo ancora con il metodo dell'analisi supponiamo il problema risolto come in figura. Conduciamo dal punto B la tangente che interseca la retta TZ nel punto K. Essendo GTZ = BHG = KBG (la prima uguaglianza segue dal parallelismo delle rette BH e TZ, la seconda perché i due angoli insistono sul medesimo arco) i due triangoli ZBK e ZTG sono simili e sussiste la proporzione ZB : ZT = KZ : GZ. Quindi ZT·KZ=ZB·GZ, ma il prodotto al primo membro dipende solo da Z e dal cerchio dato essendo uguale al quadrato del segmento di tangente condotto da Z e in definitiva il punto K risulta determinato unicamente dai dati del problema. Si osservi anche che dall' uguaglianza degli angoli GTZ e KBG segue che i punti K, B, G, e T appartengono ad una medesima circonferenza.

Trovato K, B è determinato come punto intersezione della retta tangente condotta da K alla circonferenza.

Costruzione:

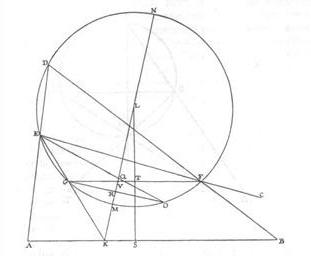
Seguendo Pappo, determiniamo dapprima il punto G, in dipendenza da T e Z e dal cerchio c di centro O. Scegliamo ad arbitrio un punto G' sulla circonferenza e congiungiamo G' con Z intersecando la circonferenza in B'. Tracciamo la circonferenza per i punti T, G', B' che interseca la retta TZ nel punto K. K dipende solo da T, Z e dal cerchio c, ma non dal punto G' (provare a muovere G' sulla circonferenza c). Da K mandiamo la tangente alla circonferenza C che interseca c in B (B è una delle intersezioni del cerchio c con il cerchio di diametro KO). Congiungiamo B con Z e determiniamo G come intersezione della BZ con la circonferenza c, e H come intersezione della TG con la circonferenza c. Verificare con Cabri che la retta BH è parallela a TZ.

Determiniamo ora il punto T nel modo seguente. Consideriamo un punto A' arbitrario sulla circonferenza c e sia G' l'altra intersezione della retta A'E con la circonferenza. Tracciamo la circonferenza passante per i tre punti A', G', D. T è l'altra intersezione della circonferenza A'G'D con la retta DEZ. Si osservi che T è indipendente da A' facendolo muovere sulla circonferenza c.

A partire da T e Z, con la costruzione precedente si determinano i punti B e G e quindi il terzo vertice del triangolo inscritto come l'altra intersezione della retta EG con la circonferenza c. Verificare con Cabri che la retta AB passa per D.

_______________________

Pappus d'Alexandrie, La Collection mathématique, Paul Ver Eecke, Paris 1933

A. Fiocca, Ricerche geometriche di Gianfrancesco Malfatti, in Gianfrancesco Malfatti nella cultura del suo tempo, Università degli studi di Ferrara 1982, pp. 159-177