Mascheroni, Bonaparte e la geometria del compasso (1797)
E' legato al nome di Napoleone un teorema che appartiene ad un'opera di Lorenzo Mascheroni, La geometria del compasso (Pavia, Galeazzi, 1797), in cui tutte le costruzioni della geometria euclidea sono realizzati senza la riga e con l'uso del solo compasso, ossia fanno intervenire al posto della retta e del cerchio, il solo cerchio. Non tutti i problemi elementari svolti col solo compasso hanno una costruzione semplice. Una delle costruzioni più interessanti è quella che permette di trovare il centro di un cerchio dato.
Lorenzo Mascheroni, membro della Commissione per la Costituzione della Repubblica Cisalpina mentre redigeva La geometria del compasso, comunicò a Napoleone, che era molto interessato alla matematica, diversi suoi risultati. Il generale, tornato in Francia, fece sfoggio di queste conoscenze geometriche in una riunione presso il Ministro degli Interni davanti a Lagrange e Laplace, che sembra aver commentato: "Tutto ci aspettavamo da lei generale, tranne che una lezione di matematica".
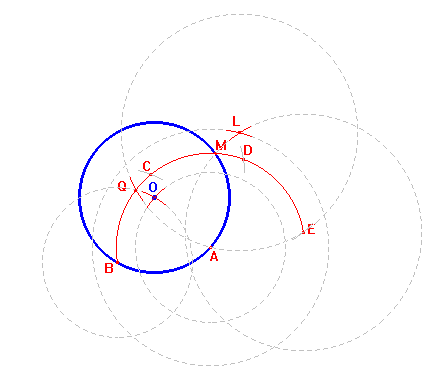
Trovare con l'uso del solo compasso il centro di un cerchio dato MAB.
Soluzione
Fatto centro in qualche punto A della circonferenza del cerchio dato, con un raggio arbitrario AB, minore del diametro del cerchio e maggiore del suo quarto, si descriva la semicirconferenza BCDE, ponendo AB = BC = CD = DE. Sia M il punto dove questa taglia la circonferenza del cerchio dato. Con raggio EM e centri E ed A, si traccino due archi che si taglino in L. Con lo stesso raggio LA e con centro L si tagli il cerchio BME in Q. Con raggio BQ e centri B ed A, si traccino due archi che si taglino in O. O è il centro cercato.
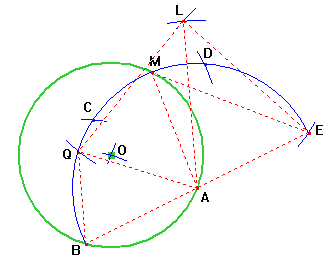
Dimostrazione
Essendo B, A, E allineati, l'angolo esterno LAB è uguale alla somma dei due angoli interni ALE e AEL del triangolo ALE. Ne segue che i triangoli LAE e LAQ hanno tutti i lati uguali e quindi hanno uguali gli angoli opposti ai lati uguali, e quindi AEL = QAL e ALE = ALQ. Dunque LAB = QAL + QLA. Sottraendo ad entrambi i membri l'angolo QAL, risulta QAB = QLA. Pertanto nel triangolo LAQ la somma dei due angoli rimanenti LAQ, LQA sarà uguale alla somma dei due angoli AQB, ABQ nel triangolo ABQ. Ma i due triango LAQ, ABQ sono isosceli per costruzione, dunque gli angoli alla loro base sono uguali alla semisomma e perciò tutti uguali tra di loro. I due triangoli LAQ e ABQ saranno dunque simili e varrà la proporzione tra i lati LA : AQ = AQ : QB. Per costruzione ME = LA e QB = OB, quindi sostituendo si ha ME : EA = AB : OB. Dunque i triangoli isosceli MAE, AOB avendo i lati proporzionali sono equiangoli e risulta l'angolo OAB = AME = AEM. Ma nel triangolo AEM l'angolo esterno MAB è uguale alla somma degli angoli interni non adiacenti per cui MAB = AME + AEM = 2 OAB. Ne segue OAB = OAM. Per il primo criterio i triangoli OAB e OAM sono dunque congruenti e in particolare risulta OB = OM. Concludendo OB = OA = OM perciò O è il centro che si cercava del cerchio MAB.