Assi radicali
Le proprietà elementari del cerchio e della sfera sono contenute nelle opere di Euclide e di Archimede, ma la cosiddetta geometria dei cerchi e delle sfere che studia insiemi infiniti di tali enti, ed in particolare i sistemi lineari (fasci) ebbe origine soltanto nei primi decenni dell’Ottocento, in connessione coi nuovi metodi sintetici ed analitici che portarono al rinnovamento della geometria, avvalendosi dei contributi di Monge, Gaultier, Gergonne, Poncelet, Steiner, Dupin, Chasles. La fondazione delle relativa teoria delle inversioni circolari si deve a Möbius, Plücker, Thomson, Liouville, Reye. Anche in questo caso molti teoremi piani possono seguire dall’analogo teorema tridimensionale (metodo fusionista).
Il termine "asse radicale" pare sia stato coniato da Louis Gaultier nel 1813 (Journal de l'École Politechnique).
La teoria degli assi radicali venne inserita nei trattati di geometria elementare per le scuole secondarie superiori della seconda metà dell'Ottocento (G. Lazzari e A. Bassani, Elementi di geometria, Livorno, Giusti, 1891).
Teorema A. Il luogo dei punti di un piano, tali che i segmenti tangenti condotti da essi a due circoli, non concentrici, siano uguali, è la parte di una retta perpendicolare alla retta dei centri dei due circoli, esterna ai circoli dati.
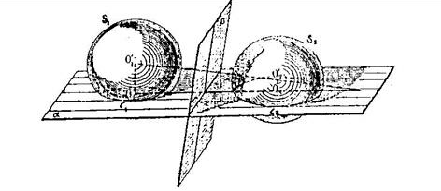
Teorema B. Il luogo dei punti tali che i segmenti tangenti condotti da essi a due sfere uguali siano uguali, è la parte, esterna alle due sfere, del piano perpendicolare al segmento congiungente i centri, nel suo punto di mezzo.

Teorema C. Dati due circoli in un piano non concentrici:
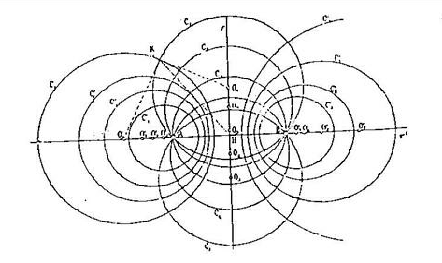
1) Esistono infiniti circoli che, presi a due a due, hanno per asse radicale la retta dei centri dei due circoli dati; il luogo dei loro centri è l’asse radicale dei due circoli dati.
2) Esistono infiniti circoli che, presi a due a due, hanno per asse radicale quello dei dei due circoli dati; il luogo dei loro centri è la retta dei centri dei cerchi dati.
1) Esistono infinite superfici sferiche che, prese a tre a tre, hanno per asse radicale la retta dei centri delle due sfere date; il luogo dei loro centri fa parte del piano radicale delle due superfici sferiche date.
2) Esistono infinite superfici sferiche che, prese a due a due, hanno per piano radicale quello delle due superfici sferiche date; il luogo dei loro centri fa parte della retta dei centri delle due sfere sfere date.
L'asse radicale di due cerchi si trova come perpendicolare alla retta dei centri, per il punto di mezzo del segmento di tangente comune ai due cerchi.