La retta di Eulero
Eulero (1707-1783) ha dato contributi di nuove conoscenze a quasi ogni branca della matematica pura e applicata, da quella elementare a quella superiore. In geometria elementare piana in particolare ha dimostrato il teorema valido per ogni triangolo (Solutio facilis problematum quorundam geometricorum difficillimorum, 1765):
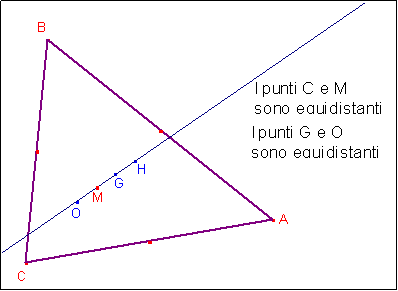
L’ortocentro, il baricentro e il circocentro di un triangolo sono allineati e il baricentro è situato tra ortocentro e circocentro a distanza doppia dall’ortocentro rispetto al baricentro.
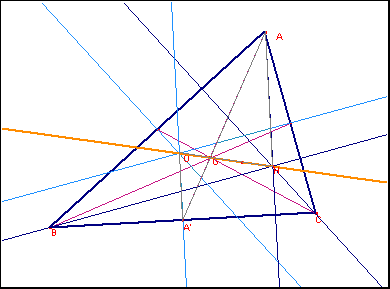
Se il circocentro O e il baricentro G del triangolo coincidono ogni mediana è perpendicolare al lato che biseca e il triangolo è “isoscele tre volte”, ossia è equilatero. Ora, se il triangolo ABC non è equilatero, il suo circocentro e il suo baricentro definiscono la retta OG (retta di Eulero), sulla quale consideriamo un punto H tale che OH=3 OG, cioè GH=2 OG.
Poiché è anche GA=2 A’G, i triangoli A’OG e AHG sono simili e dunque AH è parallelo ad A’O, che è l’asse del lato BC. Analogamente BH è perpendicolare ad AC, e CH ad AB.