Brianchon,
Poncelet,
Feuerbach
La rinascita delle ricerche di
geometria pura, dapprima in Francia, poi in tutta Europa, caratterizza i primi
decenni del sec. XIX. Si deve a due allievi di Monge, Jean-Victor Poncelet e
Charles Julien Brianchon, quello che fu detto “il più bel teorema di geometria
elementare” scoperto dai tempi di Euclide fino ad allora (1820-21):
La circonferenza che
passa per i piedi delle perpendicolari, abbassate dai vertici di un
qualsiasi triangolo sui lati opposti, passa anche per i punti di mezzo di
questi lati, oltre che per i punti di mezzo dei segmenti che congiungono i
vertici con il punto di intersezione delle perpendicolari.
|
Nel 1822 Karl Wilhelm Feuerbach dimostrò anche che il
centro della circonferenza dei nove punti giace sulla retta di Eulero tra
l’ortocentro e il circocentro, a ugual distanza da essi, ed inoltre
che essa è tangente internamente al cerchio inscritto ed esternamente
ai tre cerchi ex-inscritti.
|
 |
Alcune costruzioni parziali che concorrono alla
realizzazione della figura precedente sono illustrate nelle seguenti:
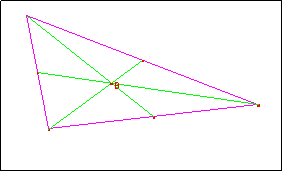
Baricentro |

Incentro |
|
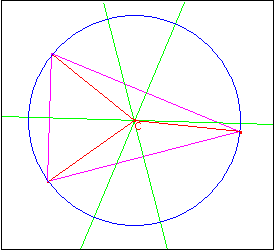
Circocentro
|

Ex-incentro
|