Ceva, Teorema di Ceva

De lineis rectis se invicem secantibus statica constructio, 1678

Gli studi di geometria sintetica vantano in Italia più che altrove una lunga tradizione. Anche in secoli di profonda innovazione nel campo della matematica come il Seicento (geometria analitica, teoria degli indivisibili, sviluppo della meccanica) o il Settecento (sviluppi del calcolo differenziale integrale e loro applicazioni al sistema del mondo) compaiono ricerche interessanti di geometria pura.

Ricordiamo qui la prima opera di Giovanni Benedetto Ceva (1647-1734) contenente un famoso teorema che porta il suo nome. Altri autori pervennero al medesimo teorema, come Johan Bernoulli, Lazare Carnot, Gaspar Coriolis, ma fu Michel Chasles che per primo nel 1837 diede risalto all'opera di Ceva. Il teorema anticipa alcuni concetti di geometria proiettiva e di calcolo baricentrico.

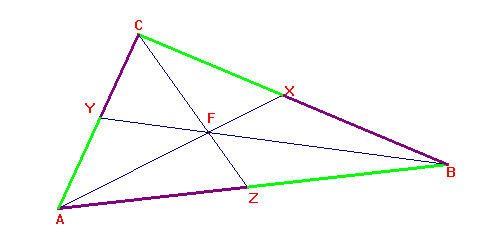
Teorema: Condizione necessaria e sufficiente affinché in un triangolo ABC le congiungenti i vertici A, B, C con i punti X, Y, Z sui lati opposti siano concorrenti è che:

AZ . BX . CY _{= +1}

ZB   XC   YA

ossia       AZ∙BX∙CY= ZB∙XC∙YA 

In altri termini, considerati i sei segmenti determinati sui lati dai punti X, Y, Z, il prodotto di tre di essi non aventi punti in comune è uguale al prodotto degli altri tre.

Corollario: Se da un punto F interno ad un triangolo ABC si conducono tre segmenti AX, BY, CZ dai vertici ai lati opposti, il punto F divide ciascuno di essi in due parti tali che: la somma dei rapporti delle parti non contenenti i vertici con gli interi segmenti è uguale a 1, ossia

FX/AX + FY/BY + FZ/CZ = 1

e la somma dei rapporti delle parti contenenti i vertici con gli interi segmenti è uguale a 2, ossia

FA/AX + FB/BY + FC/CZ = 2 .

La formulazione di Ceva si basava sui principi della statica e affermava che:

applicati ai vertici A, B, C i pesi p, q, r  tali che

p : q = BZ : ZA    e    p : r = CY : YA        allora      q : r = CX : XB .

ed inoltre

p : (q+r) = XF : FA             q : (p+r) = YF : FB             r : (p+q) = ZF : FC

Infatti poichè Z è il centro di gravità dei pesi p e q applicati rispettivamente in A e in B, e che Y  è il centro di gravità dei pesi p ed r applicati rispettivamente in A e in C, segue che il centro di gravità dei tre pesi, dovendo appartenere sia al segmento AX che a BY, coincide con F. Di conseguenza il centro di gravità dei pesi q ed r è l'intersezione del prolungamento del segmento AF con BC, ossia coincide con X. Analogamente si deduce che F è il centro di gravità dei pesi p e (q+r) applicati rispettivamente in A e in X da cui la proporzione p : (q+r) = XF : FA , e così per le altre.

_______________________

(Luigi Cremona, Intorno ad un'operetta di Giovanni Ceva, matematico milanese del secolo XVII, 1860)