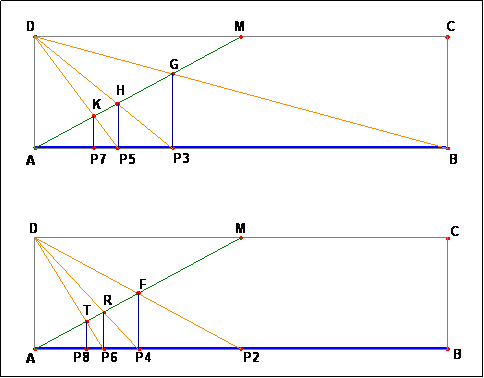
Suddivisione di un segmento in n parti congruenti

Dave e Dan, Mathematics Teacher, 1997

Nel 1997 due ragazzi statunitensi hanno dato una soluzione originale al problema della suddivisione di un segmento dato in n parti congruenti.

Essi fornirono due costruzioni diverse per n pari e per n dispari, suggerite loro dall’utilizzo di un software interattivo di geometria. La dimostrazione del loro metodo si basa su coppie di triangoli simili.

- caso di n pari

Costruzione:

Detto P₂ il punto medio di AB e M il punto medio di DC, si considerino i segmenti AM e DP₂. Sia F la loro intersezione. Il piede della perpendicolare abbassata da F su AB è il punto P₄ tale che AP₄ è la quarta parte di AB. Congiunto D con P₄ e detta R l'intersezione del segmento DP₄ con AB, P₆ è il piede della perpendicolare ad AB condotta da R. I punti P₈, P₁₀, ..., P_2n (n=1,2,...) si determinano in modo analogo.

Dimostrazione:

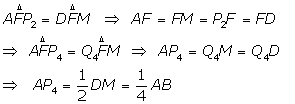
- caso di n dispari

Costruzione:

Detto M il punto medio di DC, si congiunga A con M e D con B. Dal punto G, intersezione di AM con DB, si mandi la perpendicolare ad AB. Il piede di essa è il punto P₃ tale che AP₃ è la terza parte di AB. Sia L l'intersezione del segmento DP₃ con AM. Il piede della perpendicolare condotta da L ad AB è il punto P₅ tale che AP₅ è la quinta parte di AB. I punti P₇, P₉, ..., P_2n-1 (n=1,2,...) si determinano in modo analogo.

Dimostrazione:

_______________________

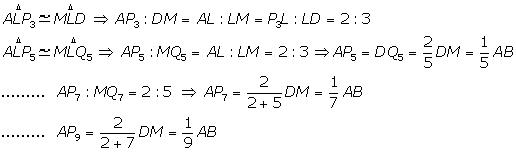
Lettera matematica Pristem, n°23, p.46