A.G.a.Fe (Algebraic Geometry at
Ferrara)
Liouville e le funzioni
meromorfe doppiamente periodiche
Abel in Recherces
sur les fonction elliptiques, scoprì la doppia periodicità della funzione φ(z)
inversa dell’integrale ellittico di prima specie e Joseph Liouville riconobbe nella doppia
periodicità una proprietà atta a caratterizzare una classe di funzioni
meromorfe più ampia di quelle introdotte da Abel. Nell’importante memoria De functionibus duarum variabilium
quadrupliciter… Jacobi aveva già mostrato che una
funzione meromorfa non può avere più di due periodi indipendenti sui reali.
Nel 1844, Liouville, in una sua comunicazione
all’Accademia delle Scienze di Parigi, mostrò come sviluppare una completa
teoria delle funzioni doppiamente periodiche (quelle che oggi sono chiamate funzioni ellittiche), fornendo una serie di teoremi generali. Un importante passo in
avanti nella diffusione della teoria secondo Liouville si ebbe nel 1847, quando
egli tenne a Parigi un corso di lezioni al quale parteciparono studiosi di
tutta Europa. In queste lezioni, oltre a dimostrare i risultati che vedremo più
avanti (senza far uso della teoria di Cauchy, ma piuttosto utilizzando la serie
di Fourier), Liouville usò implicitamente il concetto di “ordine”, che fu introdotto formalmente da Weierstrass molti anni dopo. Le note del corso di Liouville
furono publlicate a cura di C. W.
Borchardt: Leçon sur les fonctions doublement
périodiques faites en 1847 par M. J. Liouville [Journal für die Reinew und
Angewandte Mathematik, 88 (1880)].
Liouville iniziò ad interessarsi di integrali ellittici nei primi
anni del 1830. Nella memoria Sur les trascendantes elliptiques de première et de
seconde espèce, considerée comme fonctions de leur amplitude [J. Éc. Polyt. 14 (1834) 273−287], Liouville
aveva dimostrato l’impossibilità di integrare in termini finiti (cioè elementarmente)
gli integrali ellittici di primo e secondo tipo. Negli anni seguenti, queste
ricerche, condotte nell’ottica dei risultati di Legendre, indussero Liouville a
leggere le opere di Abel e di Jacobi. In particolare egli venne a conoscenza
della doppia periodicità delle funzioni inverse degli integrali ellittici di
primo tipo. In un suo quaderno di appunti, in data 1 Agosto 1844, Liouville
annotò quanto segue:
Mr Hermite
voudrait, dit-il, tirer du developpement d’une fonction f(x) en série de sinus et de cosinus la preuve de
l’impossibilité de l’existence de deux périodes réelles et incommensurable
entr’elles d’une fonction f(x) d’une
variable. Rien ne me semble plus simple [Bibliothèque de l’Institut, MS 3617 (5) p. 76v].
Ricordiamo che Jacobi aveva già provato questo risultato nella forma:
se una funzione non costante ha due
periodi essi sono necessariamente indipendenti sui reali. L’idea di Charles
Hermite, allora giovane studente, era quella di darne una dimostrazione diversa
utilizzando le serie trigonometriche. Supponiamo, in accordo con Liouville, che
f abbia due periodi α, β nei reali. Allora, rispetto ad α, f ammette il seguente sviluppo in serie
dunque, per la
periodicità rispetto a β , si ha:
Allora, per i>0, dobbiamo
avere:
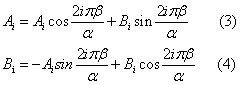
Dunque
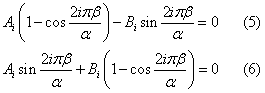
Eseguendo i quadrati e sommando si ha:
.
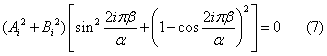Il secondo fattore è zero
se 2iπβ/α = 2mπ, ma se 
Q ciò accade solo se i
= m = 0. Dunque deve essere Ai
= Bi = 0, ossia f(x) = A0.
Nello stesso manoscritto, subito dopo, Liouville aggiunse:
si φ(x)/ ψ(x)
conserve les deux périodes 
et 
, et ne deviént jamais infinite pour x réelle ou imaginaire il ne pourrà être qu’une simple
constante. Le devéloppement en série de
sinus et cosinus le prouve.
Se φ(x)/ ψ(x) mantiene i due periodi 2ω e ,
e non viene mai infinito per x reale
o immaginario non potrà essere che una semplice costante. Lo sviluppo in serie
di seno e coseno lo provano.
È probabile dunque che
Liouville abbia scoperto il suo famoso teorema: una funzione meromorfa doppiamente periodica priva di poli si riduce ad
una costante, estendendo le argomentazioni precedenti al caso in cui il
secondo periodo β è immaginario.
Liouville passò poi ad applicare il principio precedente, “le notre principe
genéral” come
lui lo chiamava, per sviluppare una teoria delle funzioni doppiamente periodiche. Ben presto ottenne una dimostrazione del teorema fondamentale dell’algebra:
Il est bien singulier que notre principe genéral par les fonctions
à double période prouvà que toute eq.on algé briques a une racine; car si
ne devenant pas infinie, il en serait de même (y(x) etant la fonction elliptique inverse de 1er espèce) de
par suire cette dernière quantité se réducerait à un
simple constante ce qui est absurde.
E’ sorprendente che
il nostro principio generale per le funzioni a doppia periodicità conduca alla
dimostrazione del fatto che ogni equazione
algebrica ha una
radice ; se
Non diviene mai
infinito, lo stesso sarà (essendo y(x) la
funzione ellittica inversa di prima specie) di
Di conseguenza anche
quest’ultima quantità si ridurrà ad una semplice costante che è assurdo.
Come abbiamo già osservato in precedenza, nel 1847, Liouville tenne
alla Sorbona un corso di lezioni private al quale partecipò il giovane
matematico tedesco C.W. Borchard. Dalle note del corso, raccolte da
quest’ultimo, si evince a quale grado di sviluppo Liouville avesse condotto la
teoria.
Siano infatti ω1, ω2 due numeri complessi linearmente indipendenti sui
reali. Denotiamo con Г il reticolo generato da ω1, ω2 ossia
.
Ogni funzione meromorfa f in C
tale che 
è detta funzione
ellittica rispetto a Г. Denotiamo con E(Г), l’insieme delle funzioni ellittiche rispetto a Г e poniamo 
.
I risultati principali di
Liouville si possono oggi enunciare come segue:
Teorema I Sia 
e sia Pa un
parallelogramma tale che 
non contiene poli di
f. Allora 
.
Supporremo nel seguito che data , non contenga poli di f.
Teorema II Una funzione , non costante ha in Pa
lo stesso numero di zeri e di poli (contando le molteplicità). In
particolare f(z) assume in Pa ogni valore complesso
lo stesso numero di volte.
Teorema III Sia non costante, siano a1 ,…., as e b1 …., bt
rispettivamente gli zeri ed i poli di f in Pa
, m1 ,…, ms ed n1 ,…, nt loro molteplicità. Allora:
È bene notare che Liouville non ottenne questi risultati utilizzando
il calcolo integrale sviluppato da Cauchy, ma piuttosto le serie di Fourier.
Egli dimostrò anche che ogni funzione doppiamente periodica di periodi ω1 e ω2 si può sempre
esprimere come funzione razionale di una funzione doppiamente periodica φ (x), con i medesimi
periodi e di ordine due e della sua derivata
φ'(x). Liouville ottenne
anche nuove dimostrazioni, più semplici e dirette, di vari risultati di Abel e
Jacobi riguardanti il problema della divisione.
Progetto: Andrea Del Centina Realizzazione: Francesca Braga