ProbleMATEMATICAmente - Novembre 2000

Il problema di Novembre 2000 era: 

Risolvi l'equazione 3x-[x]=8. Ricorda che [x] indica la parte intera di x, ovvero il più grande numero intero minore o uguale ad x (per esempio [6,2]=6). 

Cosa sai dire dell'equazione a x + b [x] = c, al variare di a, b, c numeri interi?

Hanno risposto in sei:

  1. Antonio Bevacqua , 3A, LS Pitagora, Rende (CS)
  2. Alberto Cornia, 5B, LS Fanti, Carpi (MO)
  3. Emanuele Spadaro, LS Galilei, Catania
  4. Daniele Urzì, 3B, LS Galilei, Catania
  5. Gianpiero Caruso, 3A, LS Boggio Lera, Catania
  6. e un anonimo (tutti i partecipanti sono pregati di includere sempre nome, cognome, classe, scuola e città nel testo della soluzione che ci mandano).
A nostro parere, il problema era abbastanza interessante perché permetteva risoluzioni e considerazioni parziali diverse. Lo si può notare proprio leggendo le sei soluzioni arrivate. 

Per chiarezza di esposizione, dividiamo il nostro commento in quattro parti:

  1. Il caso particolare. Cioè, studiare l'equazione 3x-[x]=8. 
  2. Il caso generale. Cioè, studiare immediatamente ax+b[x]=c e vedere la prima parte come una semplice applicazione.
  3. L'analisi del grafico di f(x)= ax+b[x], per ragionare su come devono comportarsi le soluzioni. Come sempre, l'osservazione del grafico serve per farsi un'idea, fare congetture e considerazioni ma non è una soluzione completa. 
  4. Un sottoproblema. Cioè, studiare quante sono le soluzioni di ax+b[x]=c.
  1. Per questa prima parte, un buon esempio di soluzione, corretta e ben esposta, è quella di Alberto Cornia. 
  2. L'approccio proposto da Daniele Urzì è il più completo e permette di vedere il primo caso come un semplice esempio.

Tutte le soluzioni proposte trascurano (o svolgono in modo frettoloso) l'analisi conclusiva dei casi particolari e del numero di soluzioni. Ad esempio, solo Emanuele Spadaro osserva che ci possono essere infinite soluzioni (nel caso in cui sia a+b=0). A questo proposito notiamo che tutti hanno diviso allegramente per a+b, senza escludere che fosse a+b=0.

Se non fosse stato così, qualcuno avrebbe sicuramente adottato la strategia (spesso ricca di informazioni) di studiare alcuni casi particolari. Qui si possono considerare i tre casi

b=0         a=0          a+b=0.

Se b=0, la soluzione c'è ed è unica: x=c/a.

Se a=0, non ci sono soluzioni, a meno che c sia un multiplo di b. In questo caso tutti i punti dell'intervallo [c/b, c/b + 1) sono soluzioni dell'equazione.

Se a+b=0, non ci sono soluzioni, a meno che c/a non appartenga all'intervallo [0,1). In questo caso le soluzioni sono x_k=k + c/a, con k un numero intero.

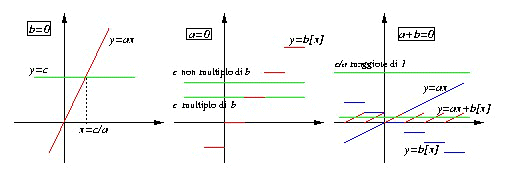
c. Ispirati dai casi particolari, si può adottare il seguente approccio grafico al problema: è evidente che i tre casi particolari sono rappresentati dai tre grafici seguenti

Nel seguito, supporremo allora che siano diversi da zero a, b e a+b. In particolare non è restrittivo supporre a>0 (altrimenti si cambia segno a tutta l'equazione). In generale, il problema che vogliamo considerare è quello di intersecare il grafico di f(x)= ax+b[x] con la generica retta orizzontale di equazione y=c. 

Se anche b è positivo, il grafico di f(x)= ax+b[x] diventa 

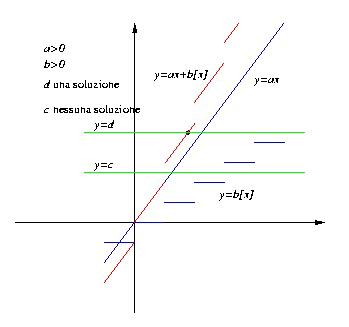
Dal quale si vede che le soluzioni sono nessuna o una, a seconda di quanto vale c. 

Se invece b è negativo, il grafico di f(x)= ax+b[x] è

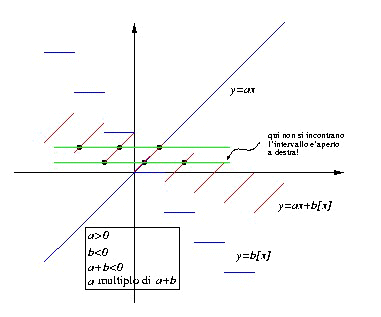
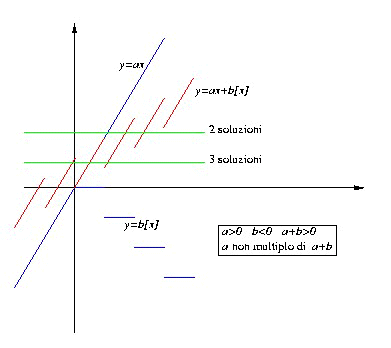
Sulla base di questo, si vede che: esiste sempre almeno una soluzione; il numero di soluzioni oscilla tra due valori n e n+1, dove n dipende solo da a e da b.

d. Da queste osservazioni, può partire l'analisi del numero delle soluzioni di ax+b[x] = c.

Come ha fatto Gianpiero Caruso, le soluzioni sono date dagli x la cui parte intera [x] appartiene all'intervallo ( (c-a)/(a+b), c/(a+b)]. Come prima cosa, osserviamo che non ci sono due soluzioni con la stessa parte intera. Allora, il numero di interi nell'intervallo ( (c-a)/(a+b), c/(a+b)] è proprio il numero delle soluzioni. Tale numero è dato da N(c)= [c/(a+b)]-[(c-a)/(a+b)] se a>0 e a+b>0 (l'altro caso è analogo). Infatti, [(c-a)/(a+b)] + 1 è il più piccolo intero nell'intervallo e [c/(a+b)] è il più grande.

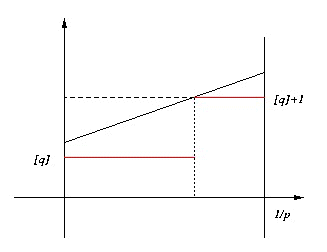
Poniamo ora z = c-a, p = 1/(a+b) e q = a/(a+b). Allora, riscriviamo la funzione N(c) come N(z)= [pz+q]-[pz] e proviamo a disegnarne il grafico. Come prima cosa, si può notare che N è una funzione periodica di periodo 1/p (infatti, la parte intera è una funzione periodica di periodo 1...). Allora è sufficiente disegnarne il grafico in [0, 1/p). 

In questo intervallo, la parte intera di pz vale sempre 0 e quindi la funzione si riduce a N(z)= [pz+q]. E questa vale [q] o [q]+1. Il che significa che il numero delle soluzioni è dato da [a/(a+b)] o da [a/(a+b)]+1. 

ndic.jpg (8627 byte)

In conclusione, il problema si prestava a tre soluzioni tutte interessanti e ad alcune considerazioni non banali sul numero delle soluzioni, che forse possono non essere alla portata di tutti. Abbiamo ritenuto utile inserirle comunque, per mostrare come sia importante che, nel risolvere un problema, si facciano anche altre osservazioni, diverse dalla semplice ricerca delle soluzioni (che spesso, semplice non è).

| Torna a ProbleMATEMATICAmente |