ProbleMATEMATICAmente - Febbraio 2000
Il problema chiedeva:
considera i primi n numeri naturali: 1, 2, … n-1, n. Indica con S1(n) la loro somma
S1(n) = 1 + 2 + … + n.
1. Ricava, con almeno due procedimenti diversi, che
![]()
2. Indica poi con S2(n) la somma dei quadrati
S2(n) = 1 + 4 + … + n2.
Ricava che
![]()
(FACOLTATIVO) Trova quindi l’espressione per la somma S3(n) dei loro cubi. E cosa puoi dire della somma Sk(n)?
Abbiamo ricevuto tre risposte da
Iniziamo analizzando il problema del calcolo di S1(n). Un metodo classico è il cosiddetto Teorema del Piccolo Gauss (vedi il libro di Bell citato nella nostra Bibliografia): scriviamo
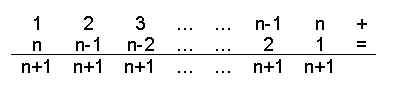
Pertanto 2S1(n) = n(n+1), da cui segue la soluzione.
Conoscendo già la formula, invece, si poteva ragionare per induzione, come hanno fatto Spadaro e Leonardi&Sottile.
Sempre Spadaro ha proposto un'interessante soluzione geometrica.
A titolo di curiosità, proponiamo poi di considerare il triangolo di Tartaglia
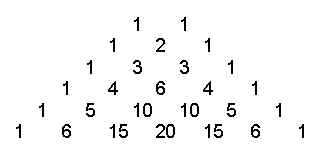
Per costruzione, la terza diagonale (1, 3, 6, 10, 15...) è composta dalle somme dei primi n numeri. Ma l'espressione del suo termine n-esimo, come si sa, e' il coefficiente binomiale
![]()
Per la seconda parte, è possibile dimostrare la formula di S2(n) per induzione, come hanno fatto, per esempio, Leonardi&Sottile.
Ci sono poi dei metodi che permettono di risolvere il problema per tutte le somme Sk(n).
Come avevamo suggerito nel testo, per calcolare S1(n) si può considerare l'identità
(h+1)2 - h2 = 2h + 1.
Se ora si sommano entrambi i membri con h che va da 1 a n, si ottiene
4 - 1 = 2 + 1
9 - 4 = 6 + 1
...
(n+1)2 - n2 = 2n + 1
e quindi
(n+1)2 - 1 = 2S1(n) + n,
da cui si ricava S1(n). Questo procedimento si generalizza: per calcolare S2(n) si considera
(h+1)3 - h3 = 3h2 + 3h + 1
e si ottiene
(n+1)3 - 1 = 3S2(n) + 3S1(n) + n.
Iterando questa tecnica si trova Sk+1(n) in funzione delle k somme precedenti.
Un metodo notevolmente migliore è stato proposto da Jacopo Stoppa di cui includiamo integralmente la risposta. La bellezza di quest'approccio sta nel fatto che si può dare un'espressione diretta alla somma Sk+1(n) che dipende solo da Sk(n):
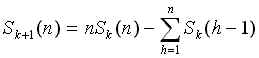
| Torna a ProbleMATEMATICAmente | Torna alla lista dei commenti |