SOMME
DI POTENZE K-ESIME DEI PRIMI N NATURALI
Jacopo Stoppa, V Sperimentale - Liceo Scientifico Statale G.Galilei, Adria(RO)
Supponiamo di conoscere la formula per la somma dei primi n naturali S(n)=n(n+1)/2
facilmente verificabile per induzione e passiamo a calcolare la somma dei primi n
quadrati.
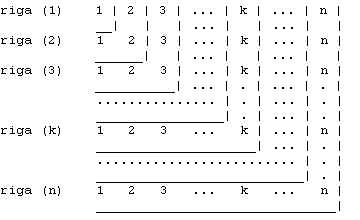
Si consideri la seguente tabella:

La somma di tutti gli interi di ogni riga è 1+2+3+...+n, cioè n(n+1)/2, e così la somma
di tutti gli interi della tabella è pari a n(n(n+1))/2. Ora sommiamo tra loro i numeri
dentro ogni regione racchiusa da linee. Per la regione delimitata dalla k-esima riga e
dalla k-esima colonna abbiamo la somma
1+2+...+(k-1)+k*k = (k-1)k/2 + k^2 = (3/2)k^2 - (1/2)k.
Sommando su tutte le regioni in questo modo ed eguagliando al risultato precedente,
otteniamo
(3/2)(1^2+2^2+...+n^2) -1/2(1+2+...+n) = n^2(n+1)/2,
da cui otteniamo 1^2+2^2+...+n^2 = (2/3)[n^2(n+1)/2 + n(n+1)/4] = n(n+1)(2n+1)/6, c.v.d.
Per la somma dei cubi consideriamo la seguente tabella:

La somma di tutti gli interi di ogni riga della tabella è 1^2+2^2+3^2+...+n^2, cioè,
n(n+1)(2n+1)/6. Dunque la somma di tutti gli interi della tabella è n^2(n+1)(2n+1)/6.
Inoltre, la somma degli interi nella regione delimitata dalla k-esima riga e dalla k-esima
colonna è pari a
1^2+2^2+...+(k-1)^2+k*k^2 = (k-1)k(2k-1)/6+k^2 = (4/3)k^3 - (1/2)k^2 + (1/6)k.
Sommando su tutte le regioni ed eguagliando al risultato precedente otteniamo
(4/3)(1^3+2^3+...+n^3)-(1/2)(1^2+2^2+...+n^2) + (1/6)(1+2+...+n) = n^2(n+1)(2n+1)/6,
da cui, dopo alcune manipolazioni ed usando il risultato per la somma dei primi n
quadrati, arriviamo a
1^3+2^3+...+n^3 = n^2(n+1)^2/4, c.v.d.
Applicando lo stesso metodo ad una tabelle di cubi, otteniamo la formula per le potenze
quarte
S^4(n) = n(n+1)(2n+1)(3n^2+3n-1)/30.
Dalla trattazione svolta, risulta evidente che per trovare S^k(n), somma delle potenze
k-esime, dobbiamo conoscere S^1(n), S^2(n), ... , S^(k-1)(n).
Ho trovato anche alcuni interessanti collegamenti con l'integrale definito, nel senso che
è possibile approssimare S^k(n) con
INT[0,n+](x^n).