Soluzione al problema di Febbraio 2000
proposta da:
Emanuele Spadaro della 3^A del LS "Galilei" di Catania
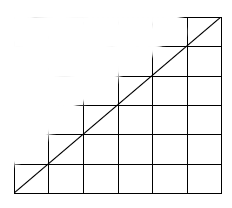
Si può ricavare pensando i numeri come dei bastoncini, cioè al numero 1 come un cubo, il numero 2 come un bastoncino con due cubi sovrapposti, il numero tre con tre cubi e così via dicendo e disporli come i figura:

Si nota che la somma da noi cercata è la somma di tutti i quadretti e quindi l'area della figura che facilmente possiamo ricavare che è:
S(n)=n^2/2 ( il mezzo quadrato di lato n)+n/2 (n volte mezzo quadratino che si trova al di là della diagonale)=n(n+1)/2