VI. 1. Massimi e minimi di Fermat

Una delle più importanti scoperte di Fermat fu descritta da lui intorno al 1629 in un trattato, rimasto inedito durante la sua vita, intitolato Metodo per trovare i massimi e i minimi. Fermat aveva considerato i luoghi geometrici espressi, in notazione moderna, da equazioni della forma ; essi sono perciò oggi noti con il nome di "parabole di Fermat" se n è positivo o di "iperboli di Fermat" se n è negativo. Per le curve algebriche della forma y = f(x) aveva elaborato un metodo molto ingegnoso per individuare i punti in cui la funzione assume un valore massimo o minimo. Confrontava il valore di f(x) in un certo punto con il valore f(x+ E) in un punto vicino. Di solito questi valori risultano nettamente diversi, ma nel punto più alto o in quello più basso di una curva continua la differenza sarà quasi impercettibile. Pertanto per trovare i punti massimo o minimo Fermat uguagliava f(x) e f(x+ E), avendo osservato che questi valori erano quasi uguali. Quanto più piccolo è l'intervallo E tra i due punti, tanto maggiormente la pseudo-uguaglianza si avvicina a una vera e propria uguaglianza; così Fermat, dopo aver diviso il tutto per E, poneva E = 0. I risultati ottenuti gli davano le ascisse dei punti massimo e minimo della curva algebrica. Questo procedimento era essenzialmente identico a quello che oggi viene chiamato differenziazione: infatti il metodo di Fermat è equivalente a trovare

e a porlo uguale a zero. E' dunque giusto, seguendo l'esempio di Laplace, proclamare Fermat creatore del calcolo differenziale. Ovviamente Fermat non possedeva il concetto di limite, ma sotto ogni aspetto il suo metodo dei massimi e dei minimi coincide perfettamente con quello oggi usato nel calcolo infinitesimale; l'unica differenza è data dal fatto che oggi, in luogo di E, si è soliti usare il simbolo h o D x.
Fermat scoprì anche il modo di applicare il suo procedimento per trovare i massimi e i minimi alla determinazione della tangente ad una curva algebrica della forma y = f(x). Se P è il punto della curva y = f(x) in cui si vuole trovare la tangente, e se le coordinate di P sono (a, b), allora un punto vicino alla curva con coordinate x = a+ E, y = f(a+ E) verrà a trovarsi così vicino alla tangente che lo si potrà considerare approssimativamente come giacente sulla tangente oltre che sulla curva.

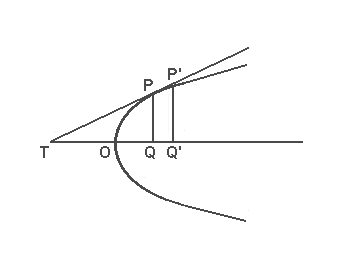Fig. 1

Se, pertanto, la sottotangente nel punto P è TQ = c (vedi Fig. 1), i triangoli TPQ e TP'Q' si possono assumere come virtualmente simili. Si ottiene così la proporzione

.

Effettuando moltiplicazioni incrociate, eliminando i termini simili, ricordando che b = f(a), dividendo poi il tutto per E e ponendo infine E = 0, si ottiene facilmente la sottotangente c. Il procedimento di Fermat equivale a dire che

è l'inclinazione della curva nel punto x = a; ma Fermat non diede una spiegazione soddisfacente del suo metodo, limitandosi a dire che era simile al suo metodo dei massimi e minimi.