VI. 4. Leonhard Euler

Dal 1727 al 1783, Euler diede il proprio contributo di nuove conoscenze a quasi ogni branca della matematica pura e applicata, da quella elementare a quella di livello più alto utilizzando un linguaggio e una notazione che per molti aspetti corrispondono a quelli usati oggi. Ad Euler dobbiamo l'uso della lettera e per rappresentare la base del sistema di logaritmi naturali o neperiani, della lettera greca 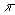per indicare il rapporto tra la circonferenza e il diametro di un cerchio, del simbolo i per indicare . 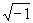Questi tre simboli danno luogo alla famosa uguaglianza 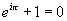(di cui possiamo vedere delle rappresentazioni attraverso frattali [77]), che contiene i cinque numeri più significativi di tutta la matematica, oltre a esprimere una importante relazione matematica. Anche nella geometria, nell'algebra, nella trigonometria e nell'analisi troviamo l'uso di simboli euleriani: l'uso delle lettere minuscole a, b, c per indicare i lati di un triangolo e delle corrispondenti maiuscole A, B, C per indicare gli angoli opposti; l'impiego delle lettere r, R, s per indicare rispettivamente i raggi dei cerchi inscritti e circoscritti a un triangolo e il semiperimetro del triangolo stesso; l'espressione lx per indicare il logaritmo di x; il simbolo 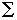per indicare la sommatoria; la notazione f(x) per indicare una funzione di x (apparsa nei Commentarii Academiae Scientiarum Imperialis Petropolitanae).
Nel valutare il progresso della matematica bisogna sempre tenere presente che i concetti che stanno dietro alle notazioni costituiscono un aspetto molto importante. Da questo punto di vista l'opera di Euler rappresenta una svolta fondamentale nella storia della matematica. Si può affermare che Euler fece per l'analisi infinitesimale di Newton e Leibniz ciò che Euclide aveva fatto per la geometria di Eudosso, o ciò che Viete aveva fatto per l'algebra di al-Khuwarizmi. Euler trattò il calcolo differenziale e il metodo delle flussioni come parti di una branca più generale della matematica che da allora è nota con il nome di "analisi" e che riguarda lo studio dei procedimenti infiniti. L'Introductio in analysin infinitorum di Euler può essere considerato come la chiave di volta dell'analisi. Questo importante trattato, uscito in due volumi nel 1748, costituì la fonte di rigogliosi sviluppi della matematica per tutta la seconda metà del XVIII secolo. Da allora il concetto di "funzione" diventò il concetto fondamentale dell'analisi. Il quarto capoverso della Introductio definisce la funzione di una quantità variabile come

una qualsiasi espressione analitica formata da quella quantità variabile e da numeri o quantità costanti.

Presumibilmente Euler aveva in mente le funzioni algebriche e le funzioni trascendenti elementari; di fatto, la trattazione rigorosamente analitica delle funzioni trigonometriche fu codificata in larga misura dall'Introductio. Il seno, per esempio, non era più un segmento, ma semplicemente un numero o un rapporto. Il primo volume dell'Introductio tratta interamente di procedimenti infiniti: prodotti infiniti e frazioni continue infinite, oltre a innumerevoli tipi di serie infinite. Da questo punto di vista l'opera rappresenta la naturale generalizzazione delle concezioni di Newton, di Leibniz e dei Bernoulli, che si erano occupati delle serie infinite. Tuttavia Euler non sempre usa tutte le cautele necessarie nell'impiego di tali serie (dettagli su questo argomento sono reperibili nel sito Giocando con le serie di Euler [78]). Anche se in qualche caso mette in guardia contro il rischio di operare con serie divergenti, egli stesso usa la serie binomiale

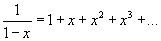
per valori di 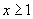. Infatti, combinando le due seri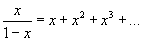e

e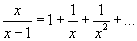

Euler concludeva che

.

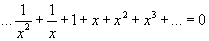Nonostante il suo uso temerario di serie infinite, operando con esse Euler riuscì a ottenere risultati che avevano sfidato ogni tentativo dei suoi predecessori. Fra questi possiamo ricordare la somma dei reciproci dei quadrati perfetti:

.

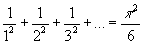Il secondo volume dell'Introductio è sulla geometria analitica. Euler comincia dividendo le curve in algebriche e trascendentali, e stabilisce una varietà si proposizioni che sono vere per tutte le curve algebriche. Classifica poi le coniche e sistema le quartiche. Infine considera la classificazione delle superfici algebriche del secondo ordine.

Euler fu, senza dubbio, il matematico che più contribuì alla elaborazione dei metodi usati oggi nei primi anni dei corsi universitari di matematica per la soluzione di equazioni differenziali. Numerosi problemi scientifici che compaiono nei manuali di uso corrente si possono far risalire ai grandi trattati sul calcolo infinitesimale redatti da Euler, le Institutiones calculi differentialis (cum eius usu in analysi finitorum ac doctrina serierum) del 1755 e le Institutiones calculi integralis (1768-1770, in tre volumi). L'uso di fattori di integrazione, i metodi sistematici per risolvere equazioni lineari di ordine superiore con coefficienti costanti, la distinzione tra equazioni lineari omogenee e non-omogenee e tra particolari e generali sono solo alcuni dei contributi dati da Euler allo studio dell'analisi infinitesimale, anche se su alcuni punti va riconosciuta una parte di merito ad altri matematici, come d'Alembert e Daniele Bernoulli. I quattro volumi delle Institutiones contenevano la più esauriente trattazione del calcolo infinitesimale che fosse mai stata presentata prima di allora. Oltre agli elementi fondamentali del calcolo e alla soluzione delle equazioni differenziali, vi troviamo il "teorema di Euler sulle funzioni omogenee" secondo il quale se f(x, y) è una funzione omogenea di ordine n, allora 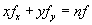, uno sviluppo del calcolo delle differenze finite, le forme normali per gli integrali ellittici e la teoria delle funzioni beta [79] e gamma [80].

Nel sito Leonhard Euler (da "Una breve spiegazione della storia della matematica " di W. W. Rouse Ball) [81], oltre alla biografia dell'autore e alle opere già citate qui, sono riportati gli scritti di Euler inerenti ad altri campi scientifici, come la meccanica, la fisica e l'astronomia.