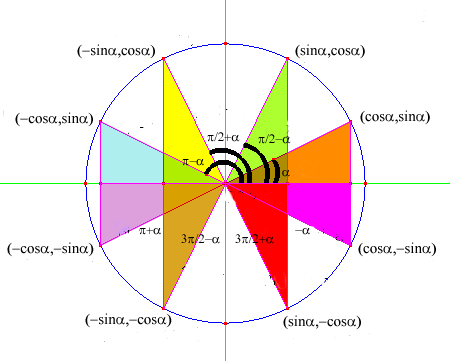
Conoscendo le funzioni goniometriche di angoli a tali che a ∈ [0,2p] è possibile dedurre immediatamente quelle degli angoli cosiddetti "associati" ad a .
Essi sono :
- angolo ( p/2 - a ), o complementare di a
- angolo ( p/2 + a ), o che differisce da a di un angolo retto
-
angolo ( p - a ), o supplementare di a
- angolo ( p + a ), o che differisce da a di un angolo piatto
- angolo ( 3p/2 - a ), o la cui somma con a è 3p/2
- angolo ( 3p/2 - a ), o che differisce da a di 3p/2
- angolo ( - a ), o opposto di a
- angolo ( 2p - a ), o esplementare di a
Osservando l'immagine della circonferenza goniometrica nella figura sopra, si possono dedurre le funzioni goniometriche degli angoli associati ad a , rappresentate dalle coordinate dei punti da essi individuati su tale circonferenza. Considerazioni di simmetria rispetto agli assi cartesiani o di uguaglianza dei triangoli colorati in figura, ci permettono di dimostrare le seguenti relazioni:
sin (p/2 - a ) = cos a
cos (p/2 - a ) = sin a
|
sin (p/2 + a ) = cos a
cos (p/2 + a ) = - sin a |
sin (p - a ) = sin a
cos (p - a ) = - cos a |
sin (p + a ) = - sin a
cos (p + a ) = - cos a |
sin (3p/2 - a ) = - cos a
cos (3p/2 - a ) = - sin a |
sin (3p/2 + a ) = cos a
cos (3p/2 + a ) = - sin a |
sin (2p - a ) = - sin a
cos (2p - a ) = cos a |
sin ( - a ) = - sin a
cos ( - a ) = cos a |
Utilizzando le relazioni fondamentali della goniometria possiamo anche dimostrare le seguenti :
tan (p/2 - a ) = cotan a
cot (p/2 - a ) = tana
|
tan (p/2 + a ) = - cot a
cot (p/2 + a ) = - tan a |
tan (p - a ) = - tan a
cot (p - a ) = - cot a |
tan (p + a ) = tan a
cot (p + a ) = cot a |
tan (3p/2 - a ) = cot a
cot (3p/2 - a ) = tan a |
tan (3p/2 + a ) = - cot a
cot (3p/2 + a ) = - tan a |
tan (2p - a ) = - tan a
cot (2p - a ) = - cot a |
tan ( - a ) = - tan a
cot ( - a ) = - cot a |
|