I più comuni tipi di proiezioni

Rispetto alle loro proprietà prevalenti, le proiezioni si distinguono in equidistanti, equivalenti e conformi, a seconda che mantengano inalterate le distanze, le aree o gli angoli. Al variare dei principi usati per la loro realizzazione, le proiezioni si dividono in vere e convenzionali. Le vere si basano su principi geometrici e matematici. Le convenzionali, seppure derivate dalle vere, utilizzano espedienti che minimizzino le deformazioni o permettano di giungere a risultati prefissati.

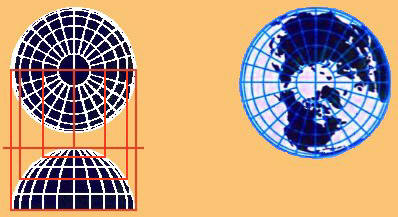
Proiezione ortografica

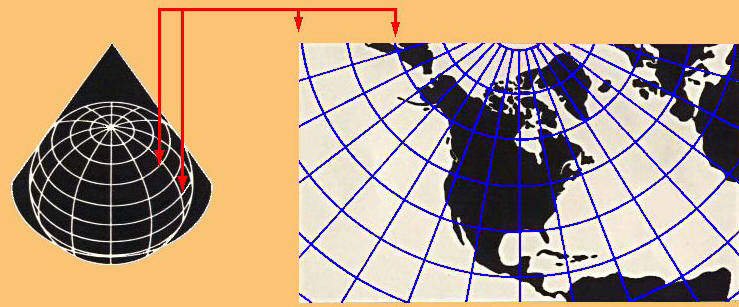
Proiezione conica centrale di Lambert

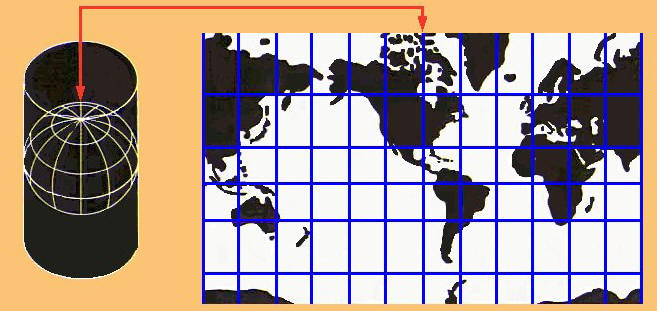
Proiezione cilindrica, rappresentazione di Mercatore

Le figure a lato presentano le proiezioni:

- prospettiche, ottenute mediante un piano tangente alla sfera in un punto qualunque della stessa e al variare del punto di osservazione, si distinguono in:

centrografica (il punto di osservazione coincide con il centro della sfera e si proietta sul piano della carta gnomonica polare);

stereografica (il punto di osservazione è sulla superficie della sfera opposta al piano di proiezione);

ortografica (all'infinito e si proietta sul piano tangente al polo opposto).

- coniche si realizzano proiettando i punti della sfera su un cono tangente ad un parallelo.

- cilindriche si ottengono avvolgendo il globo con un cilindro tangente all'Equatore.

La proiezione isogona di Mercatore è una cilindrica modificata in cui i meridiani rimangono equidistanti, mentre i paralleli, spostandosi dall'Equatore ai Poli, si allontanano reciprocamente in proporzione a quanto la distanza dei meridiani è maggiorata sulla carta rispetto alla realtà. Questa proiezione rende la carta conforme, mentre le superfici si deformano sempre più con l’avvicinarsi ai Poli (ad esempio la Groenlandia appare più vasta dell'America Meridionale). Nella azimutale equivalente di Lambert, che ha il punto di osservazione all'infinito, i meridiani sono rettilinei e perpendicolari all'Equatore, i paralleli invece si infittiscono a mano a mano che si avvicinano al Polo, il quale risulta essere un segmento e non un punto. Nell'equidistante di Delisle, una delle proiezioni coniche maggiormente usate, il cono è secante alla sfera lungo due paralleli medi della zona da rappresentare.

Per una ben fornita galleria di immagini di mappe cartografiche si può consultare il sito [12]

Tra le numerose proiezioni, nessuna è la migliore in senso assoluto: solo lo scopo prefissato orienta sull'una piuttosto che sull'altra. In generale si può dire che le proiezioni cilindriche sono efficaci per rappresentare le zone comprese tra i Tropici; le coniche, per le latitudini medie; le prospettiche invece per le latitudini alte. Per quanto riguarda le carte topografiche d'Italia, l'IGM (Istituto Geografico Militare) adotta la proiezione cilindrica di Mercatore (UTM) o conforme di Gauss, costruita con un cilindro tangente a un meridiano e non all'Equatore. In questo modo la proiezione, teoricamente solo conforme, diventa equidistante e, entro certi limiti, anche equivalente.

Proponiamo ora una tabella con le chiavi per il riconoscimento delle principali proiezioni e illustriamo di seguito uno schema riassuntivo delle proiezioni geografiche.

TIPO DI PROIEZIONE E CARATTERISTICHE	I PARALLELI SONO…	I MERIDIANI SONO…
Piana rettangolare EQUIDISTANTE	Rettilinei orizzontali, a distanza costante e reale	Rettilinei verticali, a distanza costante, equidistanti sul parallelo base
Mercatore ISOGONICA	Rettilinei orizzontali, a distanza crescente dall’Equatore ai poli	Rettilinei verticali, a distanza costante, equidistanti sull’Equatore
Sinusoidale di Sanson EQUIVALENTE	Rettilinei orizzontali, a distanza costante e reale	Curvi sinusoidali tranne quello centrale rettilineo, tagliano i paralleli con angoli sempre più acuti man mano che ci si allontana dal meridiano centrale
Di Mollweide EQUIVALENTE	Rettilinei paralleli a distanza decrescente dall’Equatore ai poli	Ellittici a distanza costante
Ellittica di Eckert EQUIVALENTE	Rettilinei paralleli a distanza decrescente dall’Equatore ai poli: i poli sono lunghi la metà dell’Equatore	Ellittici a distanza costante, equidistanti sull’Equatore
Conica vera di Tolomeo	Archi di circonferenze concentriche a distanza costante	Semirette radiali equidistanti su uno o due paralleli base
Conica conforme di Lambert	Archi di circonferenze concentriche a distanza crescente verso i poli	Semirette radiali a distanza costante, equidistanti su uno o due paralleli base
Conica modificata di Bonne EQUIVALENTE	Archi di circonferenze concentriche a distanza costante	Curvi a distanza costante, equidistanti su tutti i paralleli
policonica	Archi di circonferenze non concentriche a distanza costante sul meridiano centrale	Curvi non concentrici a distanza costante, equidistanti su tutti i paralleli
policentrica	Considerati rettilinei	Considerati rettilinei
Globulare o di Nicolosi EQUIDISTANTE	Archi non concentrici a distanza costante sul meridiano centrale e sui bordi	Circolari a distanza costante sull’Equatore
Stereografica equatoriale ISOGONICA	Archi di circonferenze non concentriche a distanza costante verso il centro	Archi di circonferenze più ravvicinati verso il centro
Stereografica polare ISOGONICA	Archi di circonferenze concentriche a distanza decrescente verso il centro	Segmenti rettilinei radiali a distanza uguale
Ortografica equatoriale PARZIALMENTE EQUIDISTANTE	Segmenti rettilinei a distanza decrescente verso i poli	Archi di ellissi a distanza decrescente verso i bordi
Ortografica polare PARZIALMENTE EQUIDISTANTE	Archi di circonferenze concentriche a distanza decrescente verso i margini	Segmenti rettilinei radiali a distanza costante
Azimutale equivalente equatoriale di Lambert EQUIVALENTE	Circonferenze concentriche a distanza decrescente verso i bordi	Rette convergenti verso il centro
Centrografica equatoriale o gnomonica di Talete ISOGONICA CON GRAVI DEFORMAZIONI	Curve speciali a distanza rapidamente crescente verso i poli	Rette parallele a distanza crescente verso i bordi (non più di 45° a Est e Ovest)
Azimutale polare, equatoriale EQUIDISTANTE	Archi di circonferenze concentriche a distanza costante	Segmenti rettilinei radiali a distanza costante

	Proprietà	Denominazione	Esempio
1	Conserva gli angoli	Applicazione conforme	Proiezione stereografica; proiezione di Mercatore
2	Conserva le aree	Applicazione equivalente	Proiezione di Lambert; proiezione di Sanson-Flamsteed
3	Trasforma geodetiche in geodetiche	Applicazione geodetica	Proiezione centrale
4	Trasforma in rette le linee formanti angolo costante con i meridiani	Applicazione lossodromica	Proiezione di Mercatore

II problema della cartografia è così ricondotto a ricercare varie applicazioni che godano di almeno una delle proprietà elencate nello schema a fianco. Si osservi che solo la proiezione di Mercatore soddisfa simultaneamente più di una delle proprietà richieste. Per esaminare queste proiezioni, è essenziale fissare, sia sulla sfera che sul piano, un sistema di coordinate di riferimento; useremo per la sfera le coordinate geografiche (β,λ) (β latitudine, λ longitudine) e nel piano le coordinate polari (ρ,φ).