Dimensioni della Terra e misura di Eratostene

Il primo ad aver misurato la circonferenza terrestre fu Eratostene (276 - 194 a.C) ma la sfericità della Terra era già tra le convinzioni dei matematici greci come pure la grande distanza che la separa dagli altri corpi celesti.

Eratostene basò i suoi calcoli sui seguenti dati:

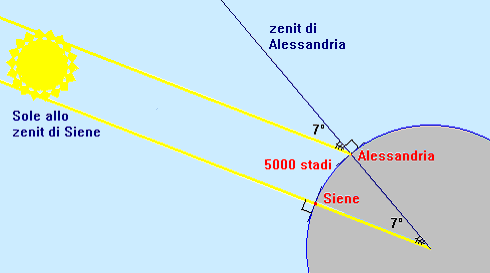
- la distanza fra Alessandria e Siene (oggi Assuan), due città sullo stesso meridiano;

- la differente altezza raggiunta dal Sole a mezzogiorno del solstizio nelle due città: mentre su Siene, prossima al Tropico, il Sole arriva allo zenit (i raggi sono perpendicolari al suolo, formando un angolo di 90°), su Alessandria esso è più basso di circa 7° (altezza di 83° sull'orizzonte).

Poiché la distanza Siene-Alessandria era di 5.000 stadi (circa 787,5 km dato che 1 stadio = 157,5 m), Eratostene stabili la relazione:

7° : 360° = 5.000 stadi : x

da cui ricavò per la circonferenza:

x = 257.142 stadi

pari a 40.500 km circa: un valore sorprendentemente vicino al vero (40.009 km). Posidonio (135 - 51 a.C.) usò lo stesso metodo partendo dalla distanza fra Rodi e Alessandria e usando la differenza di altezza della stella Canopo sul meridiano dei due luoghi calcolò una circonferenza terrestre di 240.000 stadi (38.000 km circa), valore molto vicino a quello trovato da Eratostene.

In realtà il risultato di Posidonio è dovuto alla compensazione di due errori: con i dati in suo possesso avrebbe dovuto trovare una circonferenza di 180.000 stadi.

Gli Arabi ci riprovarono nel sec. VII d. C. , quando il mondo cristiano pensava ancora a una Terra piatta, e misurarono un meridiano pari a poco più di 43.000 km. Nel 1617 l'olandese Willebrord Snell (1580 –1626) pubblicò un’opera base della geodesia nella quale propose una sua misura della Terra basata sul metodo di triangolazione. Ottenne un valore per la circonferenza terrestre di 38.600 km. Successivamente studiò anche la curva detta lossodromia, ossia il cammino sulla Terra che forma angolo costante con i meridiani.

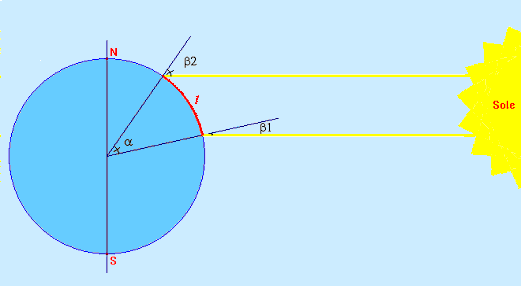
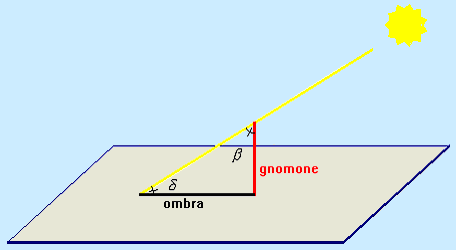
Un metodo simile a quello di Eratostene si può applicare utilizzando due luoghi distanti qualche centinaio di chilometri e situati sul medesimo meridiano, misurando in uno stesso momento le ombre di un’asta verticale (gnomone) proiettate dal Sole sul terreno.

La circonferenza terrestre si ottiene dalla proporzione:

(β₂^°-β₁^°) : 360^°= l : 2πr

se β₂ e β₁sono misurati in radianti:

(β₂-β₁) : 1 = l: r

da cui:

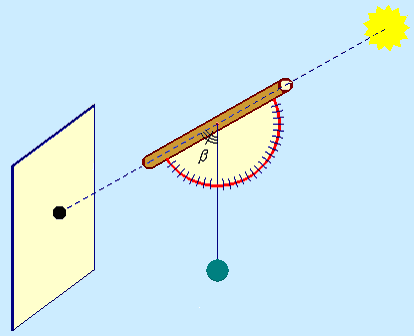
Le seguenti figure illustrano gli strumenti che si possono utilizzare per ricavare la misura dell’angolo β.