L’attività didattica proposta consiste in un momento di approfondimento e riflessione su alcune tematiche di geometria piana e solida, con il fine di mettere in risalto le potenzialità del fusionismo, in particolare utilizzando considerazioni stereometriche in dimostrazioni di proposizioni di geometria piana.
Il testo di riferimento per lo sviluppo del percorso didattico è una fonte storica originale, gli Elementi di Geometria di Lazzeri e Bassani, nella sua seconda edizione del 1898. L’opera è disponibile integralmente in versione digitale: http://mathematica.sns.it/opere/169/.
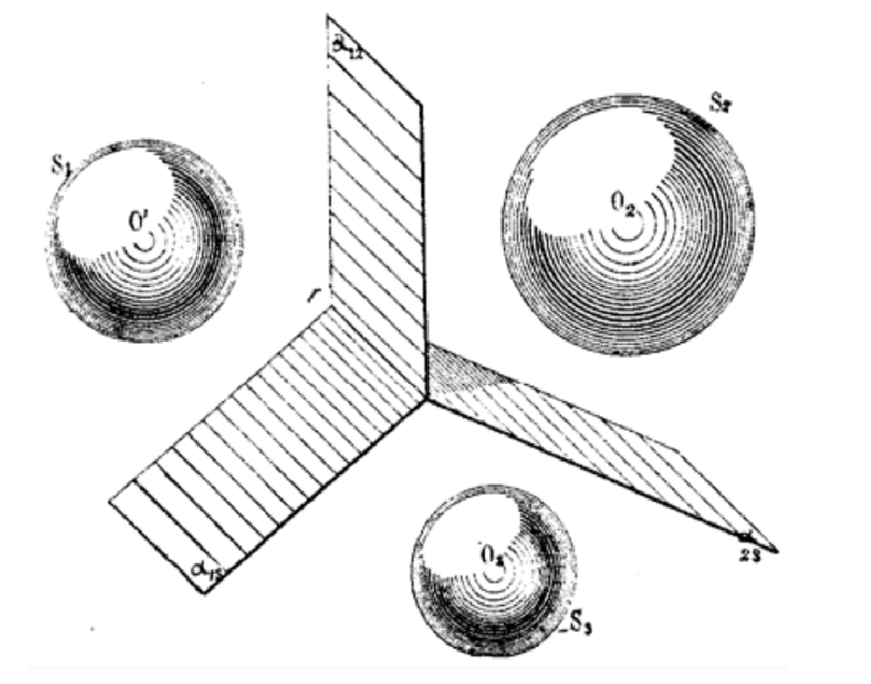
L’attività didattica proposta riguarda la Teoria degli assi radicali, la cui trattazione fusionista è particolarmente efficace. Questo tema risulta essere inoltre rappresentativo delle argomentazioni a sostegno del fusionismo, con riferimento particolare alla possibilità di trattare simultaneamente argomenti di geometria piana e solida, e alla possibilità di semplificare le dimostrazioni di alcuni teoremi di geometria piana mediante considerazioni stereometriche. Per affrontare la tematica esposta si fa particolare riferimento al Libro III dell’opera originale: Capitolo III, Sistemi di circoli e sfere.



DESTINATARI E OBIETTIVI SPECIFICI DI APPRENDIMENTO

L’attività didattica è pensata per studenti del secondo biennio di liceo di ogni indirizzo.
Nelle Indicazioni Nazionali del 2010 di tutti gli indirizzi liceali troviamo fra gli Obiettivi Specifici di Apprendimento del secondo biennio, nel nucleo Geometria, la voce seguente: «Affronterà l’estensione allo spazio di alcuni temi e di alcune tecniche della geometria piana, anche al fine di sviluppare l’intuizione geometrica. In particolare, studierà le posizioni reciproche di rette e piani nello spazio, il parallelismo e la perpendicolarità». Inoltre l’uso di fonti originali, contestualizzate da un punto di vista storico dal docente, è nuovamente in linea con tale documento. Le Indicazioni Nazionali, infatti, mettono in evidenza l’importanza di far acquisire agli studenti «una visione storico-critica dei rapporti tra le tematiche principali del pensiero matematico e il contesto filosofico, scientifico e tecnologico». Si insiste inoltre sulla possibilità di creare «collegamenti e confronti concettuali e di metodo con altre discipline come la fisica, le scienze naturali, la filosofia e la storia», attivando anche percorsi interdisciplinari.