Il teorema sui triangoli omologici
Girard Desargues, contemporaneo di Descartes, sviluppò i principi della geometria proiettiva (Brouillon projet, 1639). Messa in ombra dai successi della geometria analitica, l’opera di Desargues sarà riscoperta nell’Ottocento. Il teorema di Desargues sui triangoli omologici, tuttavia è contenuto in un'opera dell'incisore Abraham Bosse intitolata "Manière universelle de M. Desargues pour pratiquer la perspective".
Se in due triangoli ABC e A’B’C’, i vertici omologhi concorrono in un punto O (proprio o all’infinito) le rette dei lati omologhi si incontrano in punti allineati, e viceversa.
|
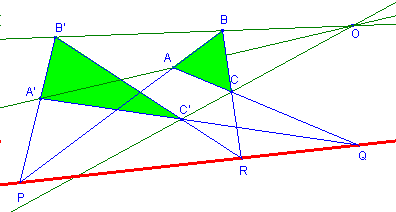
Configurazione di Desargues nel piano con centro in un punto proprio
|
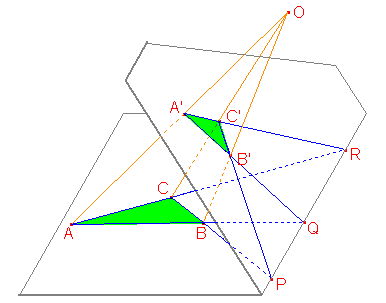
Configurazione di Desargues nello spazio
|
|
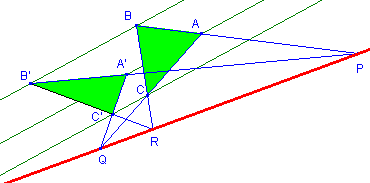
Configurazione di Desargues nel piano con centro all’infinito
|
Configurazione di Desargues nel piano con lati paralleli (retta all’infinito)
|
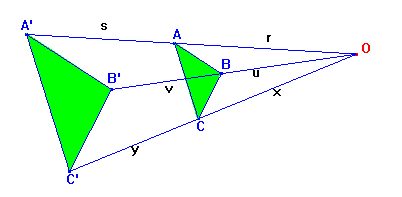
Dimostriamo il teorema in questo caso. Supponiamo che le rette congiungenti i vertici dei triangoli concorrano in un punto O e che due coppie di lati siano paralleli: AB║A'B' , AC║A'C' .
Mostriamo che anche BC e B’C’ sono paralleli, allora P, Q, R, intersezioni dei lati corrispondenti, risulteranno allineati in quanto appartenenti alla retta all’infinito.
AB ║ A'B'
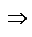u/v = r/s e AC ║ A'C'
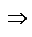x/y = r/s
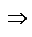u/v = x/y
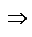BC ║ B'C'
L’implicazione inversa si dimostra in modo analogo.
_______________________
R. Courant e H. Robbins, Che cos'è la matematica? Introduzione elementare ai suoi concetti e metodi, Torino, Boringhieri, 1950, (ed. or. 1941)
